数学基础

更新: 2025/2/24 字数: 0 字 时长: 0 分钟

在计算机科学中，尤其是涉及算法、人工智能、深度学习等领域，背后都有深厚的数学基础，需要一定的数学背景知识来理解其原理和算法。所以在学习深度学习之前，复习数学知识是非常有益的。

量的部分

常量变量

• 常量：不随条件变化的量。在数学、物理等领域，常量的值在整个过程中不会变化。例如，数学中的圆周率 $\pi$ 始终为 $3.14159...$，物理学中的真空光速和重力加速度也是典型的常量。在计算机编程中，常量指程序运行时不会被修改的量。
• 变量：随条件变化的量。根据其性质，变量分为自变量、因变量。
  • 自变量：研究者可以主动操控和改变的量，用于观察它对其他变量的影响。例如，实验中改变药物的剂量，剂量就是自变量。
  • 因变量：受自变量影响而变化的量。通过观察因变量的变化来评估自变量的效果。例如，观察药物剂量对康复时间的影响，康复时间就是因变量。

提醒

在科学实验中，研究者通常通过操控自变量来观察其对因变量的影响，从而得出结论。

圆的面积

为直观说明常量和变量的区别，以圆的面积计算公式为例：

$S={\pi}r^2$

• $\pi$ 代表圆周率，其值恒定为 $3.14159...$，因此它是常量。
• $r$ 代表圆的半径，其值由计算者决定，因此它是自变量。
• $S$ 代表圆的面积，其值受到 $\pi$ 和 $r$ 共同影响，因此它是因变量。

函数部分

函数是数学中描述变量之间关系的一个基本概念。简单来说，函数是将每一个输入值与唯一一个输出值相关联的规则或关系。形式上，一个函数 $f$ 可以表示为：

$y=f(x)$

• $x$ 是自变量（输入值）。
• $y$ 是因变量（输出值）。
• $f$ 是函数，它将每个 $x$ 值映射到一个唯一的 $y$ 值。

自变量个数

根据自变量的个数，函数可以分为一元函数和多元函数。

• 一元函数（Unary Function）是只包含一个自变量的函数。在表示一元函数时，一般会写成 $f(x)$、$g(x)$、$h(x)$ 等形式，其中 $f$、$g$、$h$ 表示了自变量与函数值的对应关系。

$\begin{aligned} &f(x)=3x^2-4x+1\\ &g(x)=sin(x)+2cos(x)\\ &h(x)=e^{x-1} \end{aligned}$

• 多元函数（Multivariate Function）是指包含多个自变量的函数。在表示多元函数时，一般会使用 $g(x,y)$、$f(x,y,z)$ 等等形式表示多元函数，例如 $g(x,y)$ 是一个二元函数，$f(x,y,z)$ 是一个三元函数。

$\begin{aligned} &g(x,y)=x^2+y^2\\ &f(x,y,z)=xy+yz+zx\\ \end{aligned}$

自变量关系

根据自变量和因变量的关系，函数可以分为线性函数和非线性函数。

• 线性函数（Linear Function）是指函数图像为一条直线的函数，其通常为 $f(x) = ax + b$ 形式的函数，其中 $a$ 和 $b$ 是常数，并且 $a$ 不等于零。线性函数具有以下特性：
  1. 比例性质：如果你将 $x$ 放大 $k$ 倍，那么 $f(x)$ 也会放大 $k$ 倍。这是因为线性函数的图像是一条直线，直线上的点在平移和缩放时保持直线性。
  2. 加法性质：$f(x_1 + x_2) = f(x_1) + f(x_2)$。这表示函数值在两个输入的和上具有可加性。
• 非线性函数（Nonlinear Function）是指不满足线性函数定义的函数。它们的图像不是一条直线。非线性函数可以具有各种形状，包括曲线、波浪形等。一般而言，任何不符合 $f(x) = ax + b$ 形式的函数都被认为是非线性函数。非线性函数可能具有以下特性：
  1. 曲率：非线性函数的图像通常有曲率，而线性函数的图像总是直线。
  2. 不可加性：在一般情况下，非线性函数不满足 $f(x_1 + x_2) = f(x_1) + f(x_2)$。
  3. 复杂性：非线性函数的图像可能表现出更复杂的行为，如周期性、振荡等。

建议

在机器学习和深度学习中，非线性函数常常用于神经网络的激活函数，以增加网络的表示能力，使其能够学习更复杂的模式和关系。典型的激活函数如 ReLU（Rectified Linear Unit）就是一种非线性函数。

极限部分

极限是数学中用来描述一个量在不断变化时，接近某个固定值（极限值）的过程。简单来说，极限表示一个变量在某种条件下趋近于某个值的趋势，即使它可能永远不会真正等于这个固定值（极限值）。

案例说明

举一个案例来说明极限，看下面一个数列：在这个数列中，从左至右每一项的分母都相比前一项的分母增加了 $1$，直到第 $n$ 项的 $\frac{1}{n}$。

$\frac{1}{1},\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5}...\frac{1}{n}$

小学学过分数的我们都知道，在分子和分母都为正数时，在分子不变的情况下，分母的数值越大，整体的值就越小。这也就意味着，当 $n$ 越大时，$\frac{1}{n}$ 就越趋近于 $0$，因此我们可以写出如下等式（$c$ 为常数）：

$\lim_{n\to\infty}\frac{c}{n}=0$

按照上面的定义也可以反向使用，在分子和分母都为正数时，在分子不变的情况下，分母的数值越小，整体的值就越大。这也就意味着，当 $n$ 越小时，$\frac{1}{n}$ 就越趋近于 $\infty$，因此我们可以写出如下等式（$c$ 为常数）：

$\lim_{n\to0^+}\frac{c}{n}=\infty$

极限求解

理解了上面的两个案例后，我们看看下面两个例子如何极限求解。

• $\frac{\infty}{\infty}$ 类型的案例，解法如下：

$\begin{aligned} f(n)&=\lim_{n\to\infty}\frac{2+4+6+...+2n}{n^2}\\ &=\lim_{n\to\infty}\frac{\frac{2+2n}{2}\cdot{n}}{n^2}\\ &=\lim_{n\to\infty}\frac{n^2+n}{n^2}\\ &=\lim_{n\to\infty}1+\frac{1}{n}\\ &=1 \end{aligned}$

• $\frac{0}{0}$ 类型的案例，解法如下：

$\begin{aligned} f(n)&=\lim_{n\to\infty}\frac{\frac{1}{n^2}+\frac{2}{n^3}}{\frac{1}{n^3}-\frac{2}{n^2}}\\ &=\lim_{n\to\infty}\frac{1+\frac{2}{n}}{\frac{1}{n}-2}\\ &=-\frac{1}{2} \end{aligned}$

导数部分

导数是函数关于自变量的变化率的一种数学表示。它描述了函数在某一点附近的瞬时变化率，即当自变量发生微小变化时，函数值的变化速度。

导函数

导函数，也就是函数的导数，是描述函数变化率的函数。如果给定一个函数 $f(x)$，它的导数 $f'(x)$ 表示的就是 $f(x)$ 在 $x$ 处的瞬时变化率，即函数在该点的斜率。导函数的公式如下（$\Delta x$ 是自变量 $x$ 的一个非常小的增量）：

$f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}$

定义一个函数 $f(x)=x^2$，现求其导数 $f'(x)$ ，将其带入到导函数公式中，推导过程如下：

$\begin{aligned} f'(x) &= \lim_{\Delta x \to 0} \frac{(x + \Delta x)^2 - x^2}{\Delta x}\\ &= \lim_{\Delta x \to 0} \frac{x^2 + 2x\Delta x + (\Delta x)^2 - x^2}{\Delta x}\\ &= \lim_{\Delta x \to 0} \frac{2x\Delta x + (\Delta x)^2}{\Delta x}\\ &= \lim_{\Delta x \to 0} \left(2x + \Delta x\right)\\ &= 2x \end{aligned}$

通过推算得知，函数 $f(x) = x^2$ 的导数是 $f'(x) = 2x$，这意味着函数 $f(x)$ 在 $x$ 处的瞬时变化率为 $2x$。假设 $x = 3$，那么函数 $f(x)$ 在此处的瞬时变化率就是 $f'(x) = 2 \cdot 3 = 6$。如果此时 $x$ 增加一个非常小的量，例如 $x$ 从 $3$ 增加到 $3.01$，那么 $f(x)$ 大约会增加呢？我们可以用一个近似公式表示这个变化（$\Delta f$ 是函数值的增量），推导过程如下：

$\begin{aligned} \Delta f &\approx f'(x) \cdot \Delta x\\ &\approx 2x \cdot \Delta x\\ &\approx 2 \cdot 3 \cdot (3.01 - 3)\\ &\approx 0.06 \end{aligned}$

通过推算得知，当 $x$ 有一个非常小的增量 $\Delta x$ 时，函数 $f(x) = x^2$ 的值大约会增加 $2x \cdot \Delta x$ 这么多，所以当 $x$ 从 $3$ 增加到 $3.01$ 时，$f(x)$ 大约会增加 $0.06$。总而言之，通过 $\Delta f \approx f'(x) \cdot \Delta x$ 公式，我们可以估算出当 $x$ 增加一个非常小的量时，函数值会发生多少变化，虽然这是一个近似值，但导数给了我们一个很好的预估。

偏导数

偏导数中的“偏”，是指仅观察一个变量的改变，对整体结果的影响。在多元函数中包含了多个自变量，多元函数关于某个自变量的变化率，就是多元函数对这个自变量的偏导数。例如，多元函数 $f(x,y)$ 关于自变量 $x$ 的变化率就是 $f$ 对 $x$ 的偏导数 $\frac{\partial{f}}{\partial{x}}$， 同理多元函数 $f(x,y)$ 关于自变量 $y$ 的变化率就是 $f$ 对 $y$ 的偏导数 $\frac{\partial{f}}{\partial{y}}$。在计算某个函数关于某个变量的偏导数时，那么就只关注这个变量，将其他变量看做是常数即可。计算推导过程如下：

$\begin{aligned} &f(x,y)=x^2+y^2\\ &\frac{\partial{f}}{\partial{x}}=\frac{\partial}{\partial{x}}(x^2+y^2)=2x\\ &\frac{\partial{f}}{\partial{y}}=\frac{\partial}{\partial{y}}(x^2+y^2)=2y \end{aligned}$

了解了上面的推导过程，我们再来计算一个复杂点的二元函数 $f(x,y)$ 关于 $x$ 的偏导数 $\frac{\partial{f}}{\partial{x}}$，在推导过程中需要将 $y$ 看作常数，对各项中的 $x$ 求导，步骤如下：

$\begin{aligned} &f(x,y)=x^2+y^2+2xy+3y\\ &\frac{\partial}{\partial{x}}(x^2)=2x\\ &\frac{\partial}{\partial{x}}(y^2)=0\\ &\frac{\partial}{\partial{x}}(2xy)=2y\\ &\frac{\partial}{\partial{x}}(3y)=0\\ &\frac{\partial{f}}{\partial{x}}=2x+2y \end{aligned}$

同理，计算二元函数 $f(x,y)$ 关于 $y$ 的偏导数 $\frac{\partial{f}}{\partial{y}}$，在推导过程中需要将 $x$ 看作常数，对各项中的 $y$ 求导，步骤如下：

$\begin{aligned} &f(x,y)=x^2+y^2+2xy+3y\\ &\frac{\partial}{\partial{y}}(x^2)=0\\ &\frac{\partial}{\partial{y}}(y^2)=2y\\ &\frac{\partial}{\partial{y}}(2xy)=2x\\ &\frac{\partial}{\partial{y}}(3y)=3\\ &\frac{\partial{f}}{\partial{y}}=2y+2x+3 \end{aligned}$

计算部分

在深度学习的模型训练过程中，我们会使用一个函数来描述模型预测值与实际值之间的差距，这函数被称之为“代价函数”。代价函数通常是一个多元函数，它以模型参数（自变量）为输入，通过调整这些参数以不断逼近函数最小值为模型的优化方向。所以深度学习模型优化的核心目标，就是要计算使代价函数取得最小值时的模型参数（自变量）的取值。

极值最值

在数学中函数的“极值”和“最值”是两个不同概念，它们的区别如下：

• ‌极值‌：指的是在某一点附近的局部最大或最小值，强调的是函数在某一点附近的局部概念。
• ‌最值‌：指的是在整个定义域或特定区间上的最大或最小值，强调的是函数在给定区间的整体概念。

简而言之，极值关注的是函数在某一点的变化趋势，而最值关注的是函数在整个区间或定义域上的整体表现。

最值难点

虽然我们的最终目标是找到使代价函数取得最小值时的模型参数（自变量）的取值，但在深度学习中，我们通常不直接计算代价函数的全局最值点，而是寻找其极值点（特别是最小值点），这主要是由于以下两点原因：

1. 复杂性与不可知性：深度学习模型通常包含大量的参数，因此其代价函数通常也是一个高维的、非凸的多元函数，这意味着在高维空间中，它的形状可能包含许多峰谷、鞍点以及平坦区域，具有多个局部极小值和局部极大值。因此，直接找到全局最小值（即最值点）是非常困难的，甚至可能是不可行的。
2. 局部极值的可行性：由于深度学习模型的代价函数通常很复杂，所以我们往往只能通过优化算法（如梯度下降）找到局部极小值，而且在大多数情况下，找到的局部极小值已经能够很好地优化模型，尤其是在模型表现与训练数据的实际情况比较贴近时。实践中，局部极小值也可以为模型提供足够好的泛化性能，模型也可能在测试集上表现良好，所以全局最小值并非总是必要。

综上所述，虽然我们希望能直接计算出代价函数的全局最值点，但由于代价函数的复杂性和非凸性，直接找到全局最值点在实践中很难实现。所以在实际的深度学习中，我们会使用优化算法来找到代价函数的极值点（局部极小值），这通常也能达到足够好的模型优化效果。

必要条件

到这里我们就能明白模型优化过程，其实就是在代价函数的参数空间中寻找使函数值最小的点，即求解多元函数的极小值问题。在求解函数的极值点前，我们需要记住极值点的必要条件，也就是极值点一定会满足的条件，但满足该条件的点就不一定是极值点了。

设函数 $f(x,y)$ 在 $(x_0,y_0)$ 处有极值，如果函数在 $(x_0,y_0)$ 处有偏导数，那么该点的偏导数一定为 $0$。

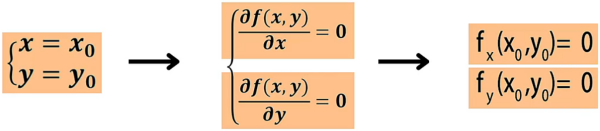
基于这个情况，我们令函数 $f(x,y)$ 所有的一阶偏导数同时为 $0$，这时可以求出具体的点 $(x_0,y_0)$，这个点被称为“驻点”。

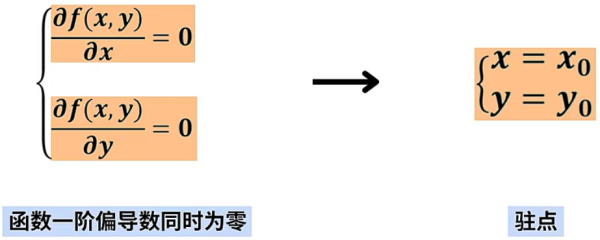
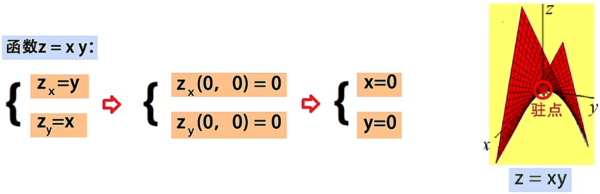
函数的极值点一定是驻点，但驻点不一定是极值点，因此驻点是极值点的必要不充分条件。为了求出函数极值点，需要先求出函数的驻点。

例如，点 $(0,0)$ 是函数 $z=xy$ 的驻点，但是从图中观察到，点 $(0,0)$ 并不是函数的极值点。

充分条件

如果要准确的判断一个驻点是极值点，还需要依赖多元函数极值的充分条件。当通过多元函数求极值的必要条件，求出函数的全部驻点后，再使用充分条件，从驻点中筛选出极值点。设函数 $f(x,y)$ 在点 $(x_0,y_0)$ 的某邻域内连续，并且有连续的一阶和二阶偏导数。 $f(x,y)$ 对 $x$ 的一阶偏导数是 $f_x(x,y)$，对 $y$ 的一阶偏导数是 $f_y(x,y)$，联立方程求出所有驻点：

接着计算 $f(x,y)$ 的二阶偏导数，也就是 $f_x(x,y)$ 对 $x$ 继续求导得到 $f_{xx}(x,y)$， $f_x(x,y)$ 对 $y$ 继续求导得到 $f_{xy}(x,y)$， $f_y(x,y)$ 对 $y$ 继续求导得到 $f_{yy}(x,y)$，将这三个二阶偏导数求出后将 $(x_0,y_0)$ 的值分别代入其中，可以得到 $A$、$B$、$C$ 三个值：

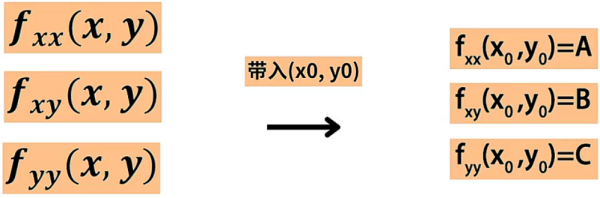
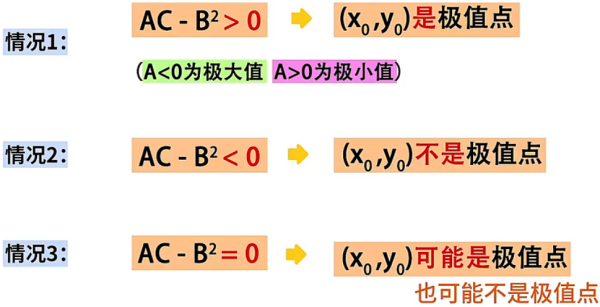
然后需要判断 $A$、$B$、$C$ 的大小关系，这里可能会出现如下三种情况（需要牢记）：

求解极值

学习了求解函数的极值点的必要条件和充分条件，最后我们求二元函数 $f(x,y)=x^3-y^3+3x^2+3y^2-9x$ 的极值点，步骤如下：

1. 求所有驻点：求函数 $f(x,y)$ 关于 $x$ 和 $y$ 的偏导数，令它们同时等于 $0$，解方程求出所有驻点，这里我们可以求出 4 个驻点。

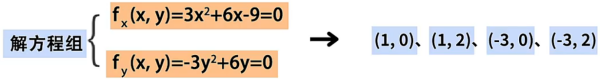
2. 带入二阶偏导：计算 $f(x,y)$ 的二阶偏导数，将这 4 个驻点带入到 3 个二阶偏导数中，可以求出 4 组 $A$、$B$、$C$ 的值。

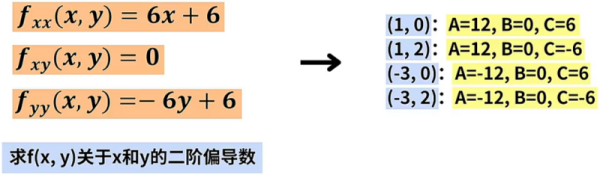
3. 判断是否是极值点：最后判断 4 组 $A$、$B$、$C$ 的大小关系，依据情况判断 $(1,0)$ 是极小值点，$(-3,2)$ 是极大值点。

建议

需要说明的是，我们可以将二元函数求极值，推广到三元函数到 N 元函数求极值，计算方法是一样的，都需要先求出驻点，再判断驻点是否是极值点。