剑眉星目

目前主要的网络模型有，深度神经网络(DNN)、卷积网络(CNN)、循环神经网络(RNN)。现在深度神经网络都是几乎都是卷积、循环两种模型的延伸。

寻找最优值

计算机是如何实现这些应用的呢？其实对于计算机来说，任何的问题都是数学问题，解决问题的方法就是所使用的算法，而解决问题的过程实质都是寻找最优值的过程。

分类分析

比如说给机器一大堆肿瘤CT照片，哪一个是良性，哪一个是恶性，都给标注清楚，然后再给机器一张新的未标注的肿瘤照片，让机器来判别这个肿瘤是良性还是恶性，这种就叫分类分析，它的本质其实也是画一条线，把良性和恶行给分开。

?> 提示：其实利用梯度下降算法来训练这个参数，非常类似于人的学习和认知过程，所谓的同化和顺应，吃一堑长一智，这就和机器学习的过程是一模一样的。

图片通道数等于1，表示黑白图片，颜色上只有一个维度；通道数等于3，表示彩色图片(RGB)，颜色上有三个维度；通道数等于4，表示在彩色图片(RGB)上加一个透明度(A)，颜色上有三个维度加一个透明维度。

图像识别

例如，在5X5的表格中，写上一个 X 字母，这对我们来说是一副图像，我们可以很轻易的认出图像中的字母，但是在计算机看来就是一大堆数，每一个格子要么黑的，要么白的，比如黑格为1，白格为0，它所代表的就是一共 $x_1$ 、 $x_2$ ...一直到 $x_{25}$ ，一共25个输入端，每个输入端输入0或1，输入完了之后，通过一系列的训练过程，计算机就能找到一大堆参数来判断它是不是一个 X 字母。

QQ截图20230613175721

?> 提示：这里幅画只有黑白两种颜色，因此我们可以用0或1来表示颜色；如果图像是灰度图，我们就可以用0~255的一个灰度值来表示颜色；如果图像是彩色图，我们就可以用RGB三个颜色，三组0~255的一个值来表示颜色。所以不管是什么图，最后都能换成一大堆的数字，我就能把这一大堆数字，放入神经元中进行训练参数，最后找到一个误差最小的函数，这就是一个成功的训练，从此以后，我利用这个参数就能判断这个图案的形状。如果只想判断这幅图是不是 X 字母，那也许一层神经元就够了。

生成数据集

生成数据集：产生批量的真实数据。

python

import random
import torch

def synthetic_data(w, b, num_example):
    """构造一个人造数据集，生成y = wx + b + 噪声"""
    # 生成均值为0，标准差为1的随机数，num_example行数，w列数
    x = torch.normal(0, 1, size=(num_example, len(w)))
    # y函数
    y = torch.matmul(x, w) + b
    # 加上噪声，均值为0，标准差为0.01，形状和y相同
    y += torch.normal(0, 0.01, y.shape)
    # 返回x和y的拍平
    return x, y.reshape((-1, 1))

# 真实的w、b
true_w = torch.tensor([2, -3.4])
true_b = 4.2
# 生成特征、标注
features, labels = synthetic_data(true_w, true_b, 1000)

读取小批量

读取小批量：定义一个 data_iter 函数，该函数接收批量大小、特征矩阵和标签向量作为输入，生成大小为 batch_size 的小批量。

python

# batch_size批量大小, features特征, labels标注
def data_iter(batch_size, features, labels):
    # 样本数量
    num_examples = len(features)
    # 生成序号
    indices = list(range(num_examples))
    # 打乱标号，这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices)
    # 随机抽取样本
    for i in range(0, num_examples, batch_size):
        batch_indices = indices[i: min(i + batch_size, num_examples)]
        # 返回随机样本的特征、标注
        yield features[batch_indices], labels[batch_indices]

batch_size = 10
for x, y in data_iter(batch_size, features, labels):
    print(x, '\n', y)
    break

初始化参数

初始化参数：初始化模型参数。

python

# 随机初始化为均值0，方差为0.01（正太分布），输入维度是2，因此size=(2, 1)
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
# 偏差（标量），因为要更新，所以requires_grad=True
b = torch.zeros(1, requires_grad=True)

定义模型

定义模型：定义模型函数。

python

def linreg(x, w, b):
    """线性回归模型"""
    return torch.matmul(x, w) + b

定义损失

定义损失：定义损失函数。

python

def squared_loss(y_hat, y):
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

定义优化

定义优化：定义优化算法。

python

# params参数里面包含w、b，lr学习率，batach_size批量大小
def sgd(params, lr, batch_size):
    """小批量随机梯度下降"""
    # 更新的时候不需要计算梯度
    with torch.no_grad():
        for param in params:
            # 学习率减去梯度再求均值
            param -= lr * param.grad / batch_size
            # 梯度置零
            param.grad.zero_()

训练函数

训练函数：设计训练函数。

python

# 学习率
lr = 0.03
# 训练轮数（一次完整的训练就是一个epoch）
num_epochs = 3
# 线性模型
net = linreg
# 损失函数
loss = squared_loss
# 每次训练都是两层
for epoch in range(num_epochs):
    # 第一层（扫描一遍数据，每次拿出一个批量大小的x，y）
    for x, y in data_iter(batch_size, features, labels):
        # 把x, w, b放进net线性模型中进行计算得到预测的y，再和真实的y做损失
        l = loss(net(x, w, b), y)
        # 损失l就是一个长为批量大小的向量，进行求和，再求导（算梯度）
        l.sum().backward()
        # 算完梯度后，使用sgd对w, b参数更新
        sgd([w, b], lr, batch_size)
    # 第二层（数据扫描完一次之后，评价一下我们的进度，这块不需要计算梯度）
    with torch.no_grad():
        # 整个的features数据传进模型，计算值和真实的labels进行比较
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
# 比较真实参数和通过训练学到的参数来评估训练的成功程度
print(f'w的估计误差：{true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差：{true_b - b}')
'''
输出：
epoch 1, loss 0.035855
epoch 2, loss 0.000131
epoch 3, loss 0.000048
w的估计误差：tensor([ 0.0003, -0.0011], grad_fn=<SubBackward0>)
b的估计误差：tensor([0.0007], grad_fn=<RsubBackward1>)
'''

简洁实现

这里我们先安装一个d2l包，下面会用到，安装命令如下：

pip install --user d2l

通过使用深度学习框架来简洁地实现线性回归模型。

python

# 导入torch的模具
from d2l import torch as d2l
import torch
# 导入nn神经网络、optim优化器
from torch import nn, optim
# 导入data数据类
from torch.utils import data

'''读取数据集，将数据集导入加载器'''
# 真实的w、b值
true_w = torch.tensor([2, -3.14])
true_b = 4.2
# 生成整个数据集
features, labels = d2l.synthetic_data(true_w, true_b, 1000)
# 通过TensorDataset将data_array打包为一个dataset
data_set = data.TensorDataset(*(features, labels))
# 通过DataLoader将dataset顺序shuffle随机打乱，再分为多个批量大小为batch_size的样本，返回一个PyTorch数据迭代器
data_iter = data.DataLoader(data_set, batch_size=10, shuffle=True)

'''定义模型线性层'''
# 使用框架定义好的Linear线性层，输入是2（输入的二维张量的大小[batch_size, 2]），输出是1（输出的二维张量的大小[batch_size, 1]，也表示全连接层的神经元个数，单层神经网络），最后放到Sequential容器里
model = nn.Sequential(nn.Linear(2, 1))
# 初始化模型w参数，通过下标0访问到Linear线性层，.weight斜率w，.data真实数据，.normal_正太分布
model[0].weight.data.normal_(0, 0.01)
# 初始化模型b参数，通过下标0访问到Linear线性层，.bias偏差b，.data真实数据，.fill_填充数据
model[0].bias.data.fill_(0)

'''定义优化器'''
# SGD随机梯度下降，net.parameters()模型参数，lr学习率
optimizer = optim.SGD(net.parameters(), lr=0.03)

'''定义损失函数'''
# 均方误差是一个常用的误差，在框架里已经自定义好了MSELoss类，也称平方L2范数
loss_function = nn.MSELoss()

'''开始3轮训练'''
num_epochs = 3
for epoch in range(num_epochs):
    # 每一次选择一个批量来计算梯度
    for x, y in data_iter:
        # 梯度清零（不清零，PyTorch会累加梯度）
        optimizer.zero_grad()
        # 计算损失，model自己本身带了模型参数w，b，因此只需传递x
        loss = loss_function(model(x), y)
        # 这里PyTorch已经做了sum()操作了，backward()反向传播
        loss.backward()
        # step()更新模型参数
        optimizer.step()
    # 调用整个features数据和labels标注，对模型损失计算
    l = loss_function(model(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')
'''
输出：
epoch 1, loss 0.000261
epoch 2, loss 0.000102
epoch 3, loss 0.000101
'''

模型训练

深度学习的核心总结起来就四个字“模型训练”。

在第一轮完整的训练结束后，会生成一个模型，由于模型只训练了一轮，因此模型的预测精度并不会很高。为了提高模型精度，我们会继续使用该模型进行第二轮、第三轮...的训练，每一轮完整的训练就称为一个“epoch”。通常每个 epoch 后都会生成一个模型，如果当前模型的预测精度高于之前模型的预测精度，则舍弃之前的模型，反之则保留当前模型以供下一轮训练使用。因此，我们最终会得到两个模型，一个是预测精度最高的模型（最适合使用的模型），另一个是最后一轮训练后得到的模型。

你的说法总体上是正确的，但有一些细节可以补充和澄清：

训练过程中的模型生成：
- 在每个 epoch 之后，模型的参数都会更新，因此在每个 epoch 后都会有一个新的模型版本。
- 这些模型版本通常在训练过程中会被保存，以便后续可以进行评估和比较。
模型的保存和选择：
- 保存最佳模型：在实际训练过程中，通常会保存表现最好的模型，即在验证集上表现最优的模型。这是因为模型的最终表现不仅取决于训练集上的表现，还需要考虑验证集上的表现，以避免过拟合。
- 更新和比较：在每个 epoch 后，通常会使用验证集评估当前模型的表现。如果当前模型在验证集上的表现优于之前保存的最佳模型，就更新保存的最佳模型。
- 最终模型：训练结束后，通常会使用在验证集上表现最好的模型作为最终模型，这个模型可能不是最后一个 epoch 的模型，而是在训练过程中所有 epoch 中表现最好的模型。
最终得到的模型：
- 最佳模型：是指在训练过程中，验证集上表现最好的模型（即预测精度最高的模型）。
- 最后一个 epoch 的模型：是指训练完成后的最终模型版本，它可能不是最优的模型，因为它未必在验证集上表现最佳。

总结来说，训练过程中会保存多个模型版本，通常会选择在验证集上表现最佳的模型作为最终模型，以保证模型在实际应用中的效果最佳。最后一个 epoch 的模型不一定是最优的，选择标准应基于验证集上的表现。

在深度学习的过程中，每个 epoch 结束后并不会自动生成一个模型文件。实际上，训练过程中模型的参数会在每个 epoch 完成时更新，但是否生成模型文件取决于开发者的设置。

通常，开发者会在训练代码中显式指定在某些条件下保存模型，例如：

每个 epoch 后保存模型：有时开发者会选择在每个 epoch 完成后保存一个模型文件。
验证集表现最佳时保存模型：更常见的做法是在训练过程中使用验证集评估模型表现，只有当模型在验证集上的性能优于之前的模型时才保存该模型。
周期性保存模型：有时为了防止训练中途出错或中断，开发者会设置定期保存模型，可能是每几个 epoch 或固定的时间间隔。

因此，严格来说，“在第一轮完整训练（一个 epoch）结束后，会生成一个模型”的说法不完全正确，是否保存模型取决于开发者的配置和具体实现。如果没有指定保存条件，模型只是经过更新，而不会自动生成可保存的文件。

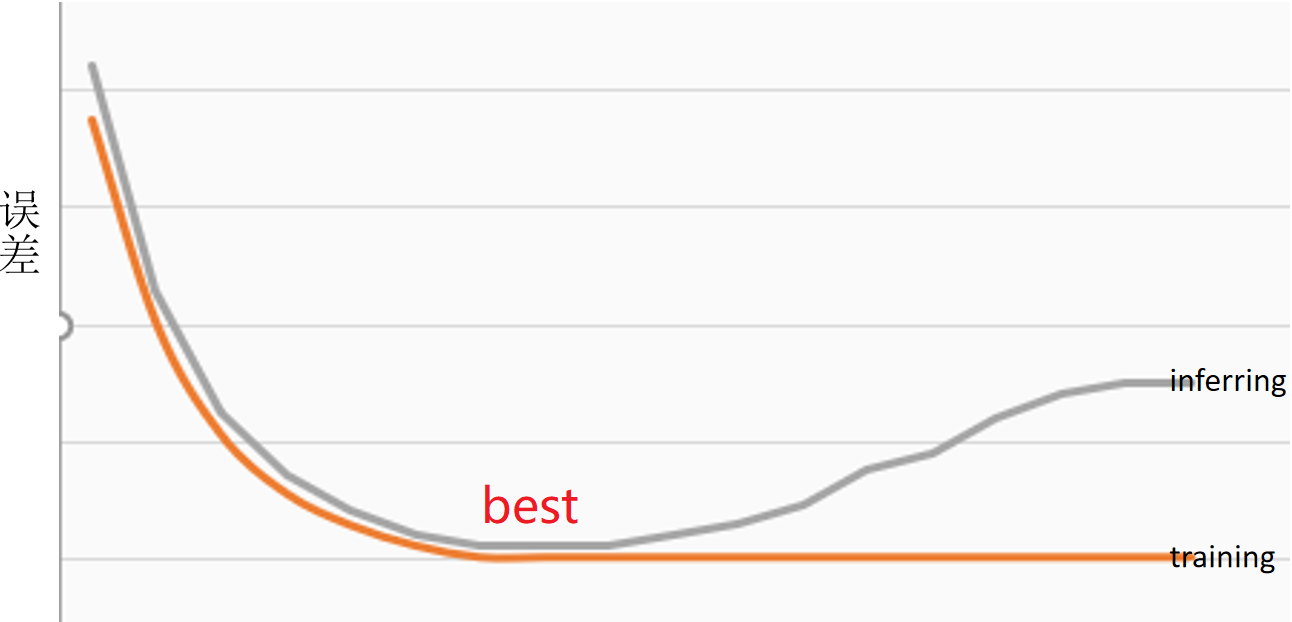
其训练与推理准确度关系大致分步如下图：当训练（Training）和推理（Inferring）最相近时，我们就认为这是最适合使用的模型。

QQ截图20221227232500

寻找最优值 ​

分类分析 ​

图像识别 ​

生成数据集 ​

读取小批量 ​

初始化参数 ​

定义模型 ​

定义损失 ​

定义优化 ​

训练函数 ​

简洁实现 ​

模型训练 ​

寻找最优值

分类分析

图像识别

生成数据集

读取小批量

初始化参数

定义模型

定义损失

定义优化

训练函数

简洁实现

模型训练