线性代数
更新: 2025/2/24 字数: 0 字 时长: 0 分钟
标量
标量,可以简单理解为一个值。
标量由只有一个元素的张量表示:
python
import torch
x = torch.tensor([3.0])
y = torch.tensor([2.0])
print(x + y) # 输出:tensor([5.])
print(x * y) # 输出:tensor([6.])
print(x / y) # 输出:tensor([1.5000])
print(x ** y) # 输出:tensor([9.])向量
向量,可以简单理解为一组值。
你可以将向量视为标量值组成的列表,通过列表的张量的索引来访问任意元素,还可以访问张量的长度、形状:
python
import torch
x = torch.arange(4)
print(x) # 输出:tensor([0, 1, 2, 3])
print(x[3]) # 输出:tensor(3)
print(len(x)) # 输出:4
print(x.shape) # 输出:torch.Size([4])矩阵
矩阵,可以简单理解为多组值。
通过指定两个分量m和n来创建一个形状为 m x n 的矩阵,通过 T 可以进行矩阵的转置:
python
import torch
a = torch.arange(20).reshape(5, 4)
print(a)
print(a.T)
'''
输出:
tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19]])
tensor([[ 0, 4, 8, 12, 16],
[ 1, 5, 9, 13, 17],
[ 2, 6, 10, 14, 18],
[ 3, 7, 11, 15, 19]])
'''特殊矩阵
对于对称矩阵来说,它的转置等于其自己:
python
import torch
B = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
print(B)
print(B == B.T)
'''
输出:
tensor([[1, 2, 3],
[2, 0, 4],
[3, 4, 5]])
tensor([[True, True, True],
[True, True, True],
[True, True, True]])
'''多轴结构
就像向量是标量的推广,矩阵是向量的推广,我们可以构建具有更多轴的数据结构:
python
import torch
x = torch.arange(24).reshape(2, 3, 4)
print(x)
'''
输出:
tensor([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
'''二元运算
给定具有相同形状的任何张量,任何按元素二元运算的结果都是相同形状的张量:
python
import torch
a = torch.arange(20, dtype=torch.float32).reshape(5, 4)
# clone()相当于是深拷贝
b = a.clone()
print(a)
print(a + b)
# 两个矩阵的按元素乘法称为“哈达玛积”
print(a * b)
'''
输出:
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]])
tensor([[ 0., 2., 4., 6.],
[ 8., 10., 12., 14.],
[16., 18., 20., 22.],
[24., 26., 28., 30.],
[32., 34., 36., 38.]])
tensor([[ 0., 1., 4., 9.],
[ 16., 25., 36., 49.],
[ 64., 81., 100., 121.],
[144., 169., 196., 225.],
[256., 289., 324., 361.]])
'''求和运算
计算元素之和,以及任意形状张量的元素和:
python
import torch
a = torch.arange(2 * 20).reshape(2, 5, 4)
print(a)
print(a.shape)
print(a.sum())
'''
输出:
tensor([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19]],
[[20, 21, 22, 23],
[24, 25, 26, 27],
[28, 29, 30, 31],
[32, 33, 34, 35],
[36, 37, 38, 39]]])
torch.Size([2, 5, 4])
tensor(780)
'''
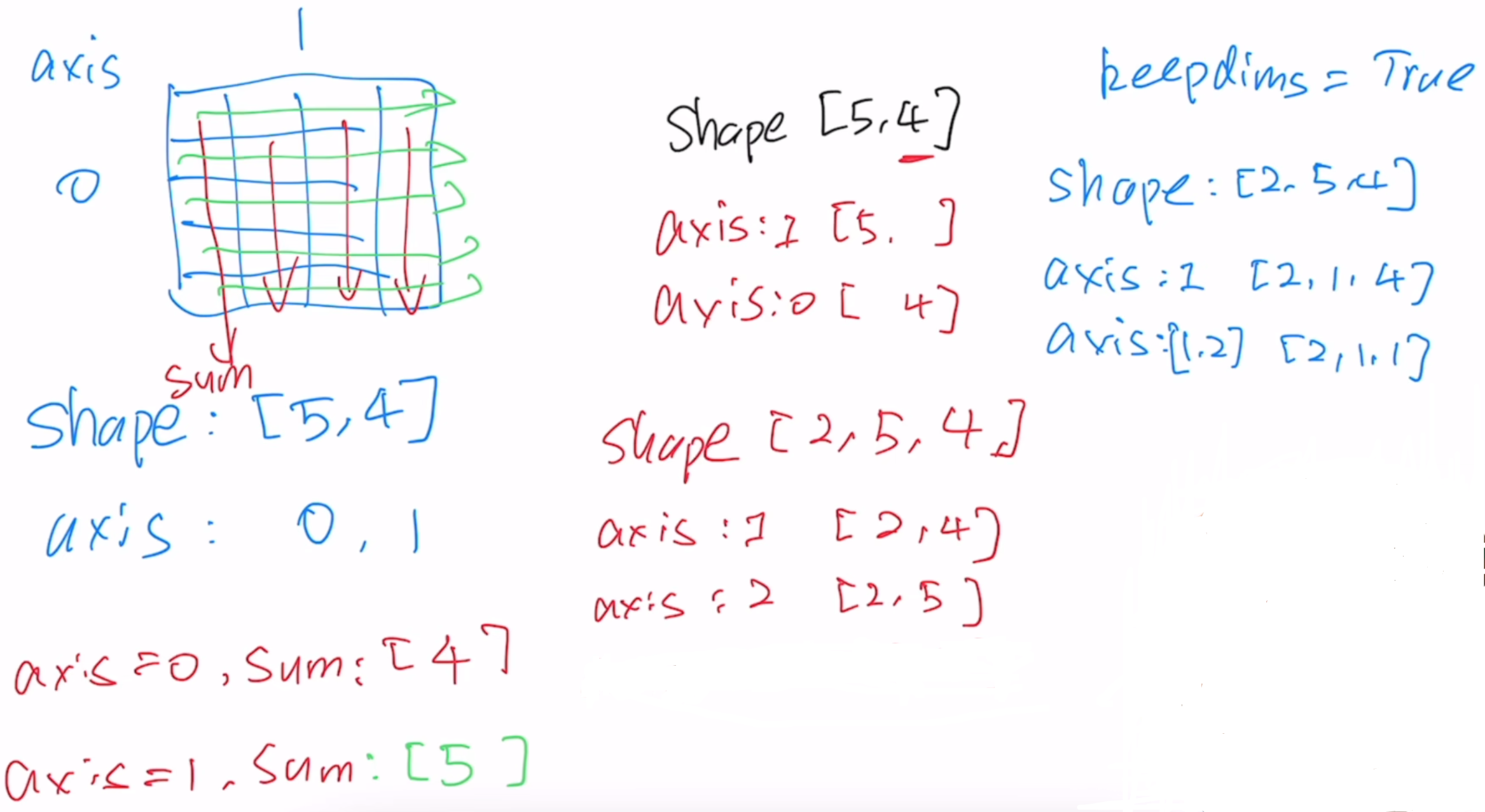
# 注释:axis代表维度,axis=0进入第一层相加,即组与组相加。
print(a.sum(axis=0))
print(a.sum(axis=0).shape)
'''
输出:
tensor([[20, 22, 24, 26],
[28, 30, 32, 34],
[36, 38, 40, 42],
[44, 46, 48, 50],
[52, 54, 56, 58]])
torch.Size([5, 4])
'''
# axis代表维度,axis=1进入第二层相加,即列与列相加。
print(a.sum(axis=1))
print(a.sum(axis=1).shape)
'''
输出:
tensor([[ 40, 45, 50, 55],
[140, 145, 150, 155]])
torch.Size([2, 4])
'''
# axis代表维度,axis=[0, 1],即先组与组相加,再列与列相加。
print(a.sum(axis=[0, 1]))
print(a.sum(axis=[0, 1]).shape)
'''
输出:
tensor([180, 190, 200, 210])
torch.Size([4])
'''
# keepdims保持数据维度不变
print(a.sum(axis=1, keepdims=True))
# 通过广播将a除以sum_a
print(a / a.sum(axis=1, keepdims=True))
'''
输出:
tensor([[[ 40, 45, 50, 55]],
[[140, 145, 150, 155]]])
tensor([[[0.0000, 0.0222, 0.0400, 0.0545],
[0.1000, 0.1111, 0.1200, 0.1273],
[0.2000, 0.2000, 0.2000, 0.2000],
[0.3000, 0.2889, 0.2800, 0.2727],
[0.4000, 0.3778, 0.3600, 0.3455]],
[[0.1429, 0.1448, 0.1467, 0.1484],
[0.1714, 0.1724, 0.1733, 0.1742],
[0.2000, 0.2000, 0.2000, 0.2000],
[0.2286, 0.2276, 0.2267, 0.2258],
[0.2571, 0.2552, 0.2533, 0.2516]]])
'''
均值运算
一个与求和相关的量是平均值:
python
import torch
a = torch.arange(2 * 20, dtype=torch.float32).reshape(2, 5, 4)
# mean平均值(数据必须是浮点数)
print(a.mean(), a.sum() / a.numel())
print(a.mean(axis=0), a.sum(axis=0) / a.numel())
'''
输出:
tensor(19.5000) tensor(19.5000)
tensor([[10., 11., 12., 13.],
[14., 15., 16., 17.],
[18., 19., 20., 21.],
[22., 23., 24., 25.],
[26., 27., 28., 29.]])
tensor([[0.5000, 0.5500, 0.6000, 0.6500],
[0.7000, 0.7500, 0.8000, 0.8500],
[0.9000, 0.9500, 1.0000, 1.0500],
[1.1000, 1.1500, 1.2000, 1.2500],
[1.3000, 1.3500, 1.4000, 1.4500]])
'''乘积运算
torch.dot 只对一维向量做乘积再进行求和,它等价于元素乘法再求和:
python
import torch
x = torch.arange(4, dtype=torch.float32)
y = torch.ones(4, dtype=torch.float32)
print(x)
print(y)
print(torch.dot(x, y))
print(torch.sum(x * y))
'''
输出:
tensor([0., 1., 2., 3.])
tensor([1., 1., 1., 1.])
tensor(6.)
tensor(6.)
'''矩阵 (m, n)和向量 (n) 的积是一个列向量 (m):
python
import torch
x = torch.ones(5, 4, dtype=torch.float32)
y = torch.ones(4, dtype=torch.float32)
print(x.shape)
print(y.shape)
print(torch.mv(x, y))
'''
输出:
torch.Size([5, 4])
torch.Size([4])
tensor([4., 4., 4., 4., 4.])
'''矩阵 (m1, n1) 和矩阵 (m2, n2) 的积是一个矩阵 (m1, n2):
python
import torch
x = torch.ones(5, 4, dtype=torch.float32)
y = torch.ones(4, 3, dtype=torch.float32)
print(torch.mm(x, y))
'''
输出:
tensor([[4., 4., 4.],
[4., 4., 4.],
[4., 4., 4.],
[4., 4., 4.],
[4., 4., 4.]])
'''范数运算
L1 范数是向量元素的绝对值之和:
python
import torch
u = torch.tensor([3.0, -4.0])
print(torch.abs(u).sum()) # 输出:tensor(7.)L2 范数是向量元素平方和的平方根,有点像勾股定理:
python
import torch
u = torch.tensor([3.0, -4.0])
# norm要求输入是浮点类型数据
print(torch.norm(u)) # 输出:tensor(5.)F 范数是矩阵元素的平方和的平方根,相当于把矩阵拉成一个向量,再求元素平方和的平方根:
python
import torch
u = torch.ones(4, 9)
print(torch.norm(u)) # 输出:tensor(6.)常用函数
torch.normal(mean, std, size) 函数返回从单独的正态分布中提取的随机数的张量,该正态分布的均值是 mean,标准差是 std,矩阵大小是 size。
python
# 从一个标准正态分布N~(0,1),提取一个2x2的矩阵
torch.normal(mean=0.,std=1.,size=(2,2))
python
# 我们也可以让每一个值服从不同的正态分布,我们还是生成2x2的矩阵
torch.normal(mean=torch.arange(4.),std=torch.arange(1.,0.6,-0.1)).reshape(2,2)
提醒
方差是各个数据分别与其和的平均数之差的平方的和的平均数,标准差是方差的算术平方根。
torch.matmul(tensor1, tensor2) 函数将两个张量相乘返回结果。
- 如果两个张量都是一维的,则返回点积(标量)。
python
tensor1 = torch.Tensor([1, 2, 3]) # 注释:参数形状(3)
tensor2 = torch.Tensor([4, 5, 6]) # 注释:参数形状(3)
ans = torch.matmul(tensor1, tensor2) # 注释:结果形状()
print(ans) # 输出:tensor(32.)。注释:1 * 4 + 2 * 5 + 3 * 6 = 32。- 如果两个参数都是二维的,第一个参数的行向量乘以第二参数的列向量,则返回矩阵-矩阵乘积。
python
tensor1 = torch.Tensor([[1, 2, 3], [4, 5, 6]]) # 注释:参数形状(2, 3)
tensor2 = torch.Tensor([[1, 2], [3, 4], [5, 6]]) # 注释:参数形状(3, 2)
ans = torch.matmul(tensor1, tensor2) # 注释:结果形状(2, 2)
print(ans) # 输出:tensor([[22., 28.], [49., 64.]])。注释:1 * 1 + 2 * 3 + 3 * 5 = 22。
tensor1 = torch.Tensor([[1, 2], [3, 4], [5, 6]]) # 注释:参数形状(3, 2)
tensor2 = torch.Tensor([[1, 2, 3], [4, 5, 6]]) # 注释:参数形状(2, 3)
ans = torch.matmul(tensor1, tensor2) # 注释:结果形状(3, 3)
print(ans) # 输出:tensor([[ 9., 12., 15.],[19., 26., 33.],[29., 40., 51.]])。注释:1 * 1 + 2 * 4 = 9。- 如果第一个参数是一维的,第二个参数是二维的,在相乘的过程中,一维参数前面会加上一个前置维度,在矩阵相乘之后,将前置维度移除;另外第一个参数按行切割得到形状和第二个参数按列切割得到形状相同或者转置后形状相同,就能进行矩阵相乘,否则就是形状错配。
python
tensor1 = torch.Tensor([1, 2, 3]) # 注释:参数形状(3),相乘的过程中加上前置维度,参数形状(1, 3)
tensor2 = torch.Tensor([[4, 5, 6], [7, 8, 9]]) # 注释:参数形状(2, 3),第二个参数按列切割,相当于3个(2, 1)
ans = torch.matmul(tensor1, tensor2) # 报错:形状错配。
tensor1 = torch.Tensor([1, 2, 3]) # 注释:参数形状(3),相乘的过程中加上前置维度,参数形状(1, 3)
tensor2 = torch.Tensor([[4, 5], [6, 7], [8, 9]]) # 注释:参数形状(3, 2),第二个参数按列切割,相当于2个(3, 1)
ans = torch.matmul(tensor1, tensor2) # 注释:结果形状(1, 2),将前置维度移除,结果形状(2)
print(ans) # 输出:tensor([40., 46.])。注释:1 * 4 + 2 * 6 + 3 * 8 = 40。
tensor1 = torch.Tensor([[4, 5], [6, 7], [8, 9]]) # 注释:参数形状(3, 2),第一个参数按行切割,相当于3个(1, 2)
tensor2 = torch.Tensor([1, 2, 3]) # 注释:参数形状(3),相乘的过程中加上前置维度,参数形状(1, 3)
ans = torch.matmul(tensor1, tensor2) # 报错:形状错配。
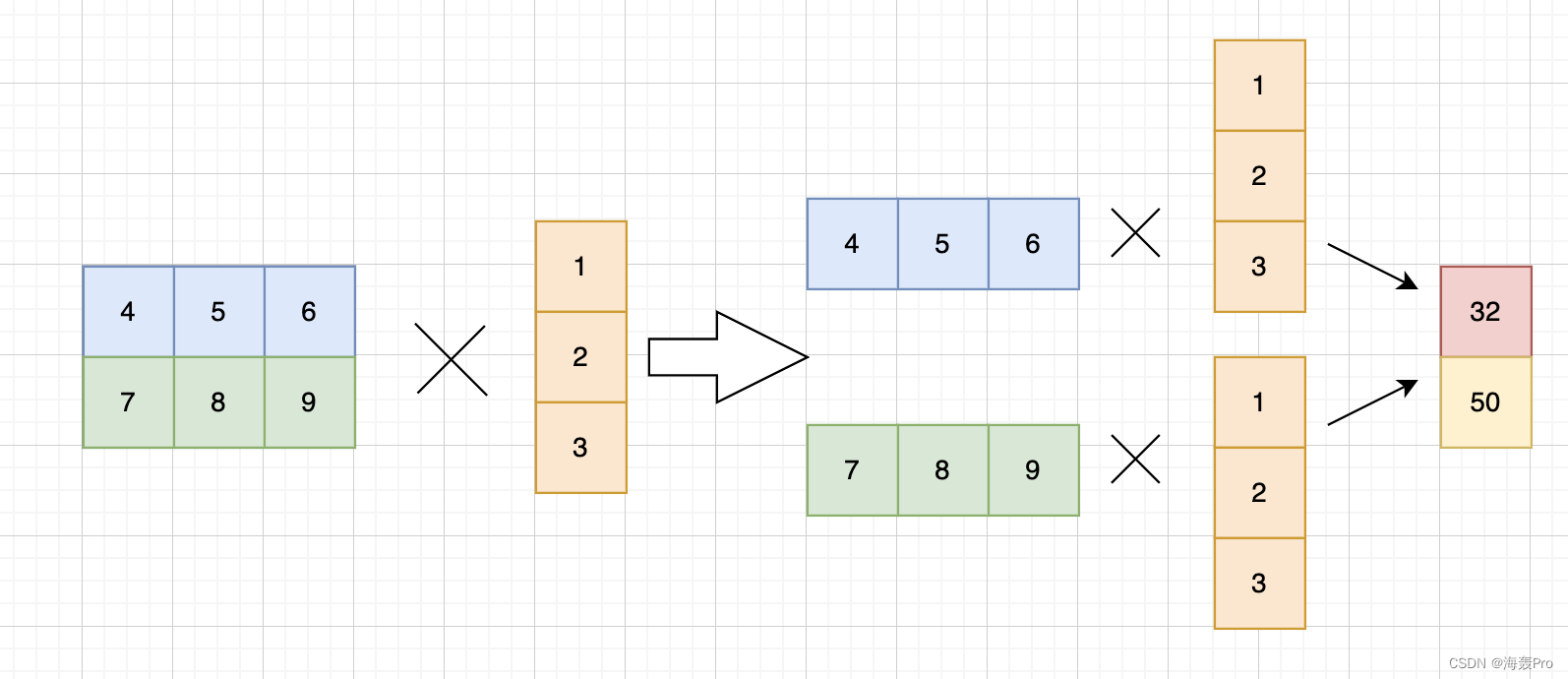
tensor1 = torch.Tensor([[4, 5, 6], [7, 8, 9]]) # 注释:参数形状(2, 3),第一个参数按行切割,相当于2个(1, 3)
tensor2 = torch.Tensor([1, 2, 3]) # 注释:参数形状(3),相乘的过程中加上前置维度,参数形状(1, 3)
ans = torch.matmul(tensor1, tensor2) # 注释:结果形状(1, 2),将前置维度移除,结果形状(2)
print(ans) # 输出:tensor([32., 50.])。注释:1 * 4 + 2 * 5 + 3 * 6 = 32。