剑眉星目

深浅模式

神经网络 ​

更新: 2025/2/24 字数: 0 字 时长: 0 分钟

在线性回归的函数模型中，我们只把面积作为了房价的影响因素，但在现实生活中房价取决于地段、面积、楼层、小区等一系列因素，那我们把这一系列因素作为一系列输入叫 x1x_1、x2x_2...xnx_n，这样一来我们就会发现房价有可能是这样一个 y=w1x1+w2x2+...+wnxn+by=w_1x_1+w_2x_2+...+w_nx_n+b 函数，其中 x1x_1、x2x_2...xnx_n 都是它的输入端，而 w1w_1、w2w_2...wnw_n 以及 bb 都是参数，这个就是一个更加详细的分析房价的一个模型，再通过一大堆的计算训练找到 w1w_1、w2w_2...wnw_n 以及 bb 这些参数的最优值让损失函数的 lossloss 值最小，这一步就需要依靠“神经网络”。

神经元 ​

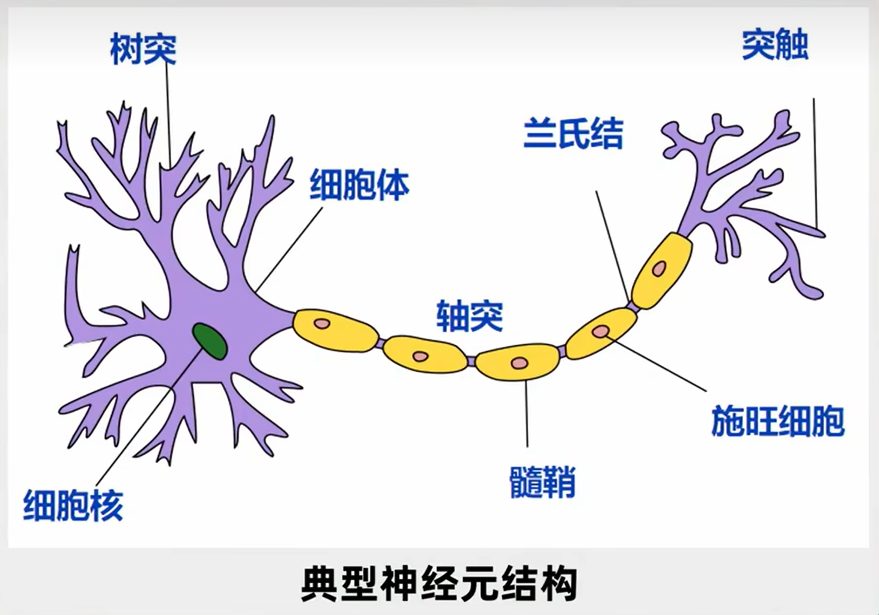
随着科学技术的发展，人类对于大脑的认知也在一步步深入。学习过生物的同学都应该知道，大脑里面有几百亿个神经元，每个神经元左边我们称之为“树突”，它用于接收上一个信号，然后这个信号经过中间的神经元叫做“轴突”，经过它的处理后，会有选择地向下释放，而向下释放的这个就叫做“突触”。因此，每个神经元都可以说是一个多输入单输出模型，就是神经元可以从多个上一级神经元中接收信号，接收到信号后进行综合处理，如果认为有必要继续输出，就会向下一级释放信号，如果认为没有必要继续输出，就不会向下一级释放信号，因此神经元输出的信号只有两种可能，要么就是 0，要么就是 1。

QQ截图20230613163223

MP模型 ​

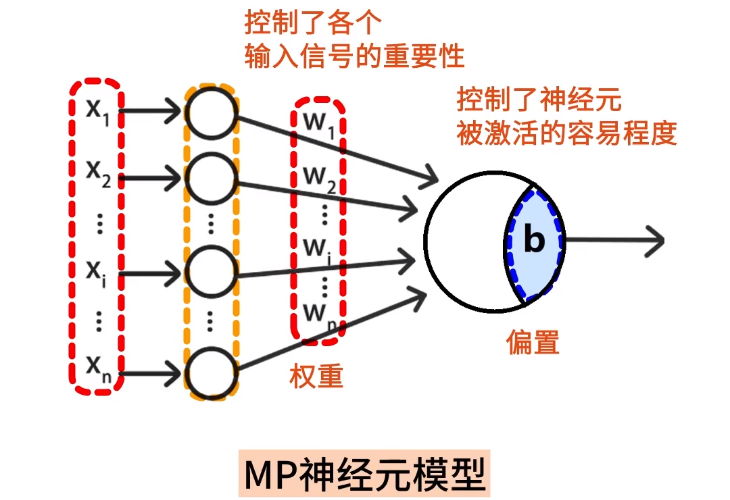
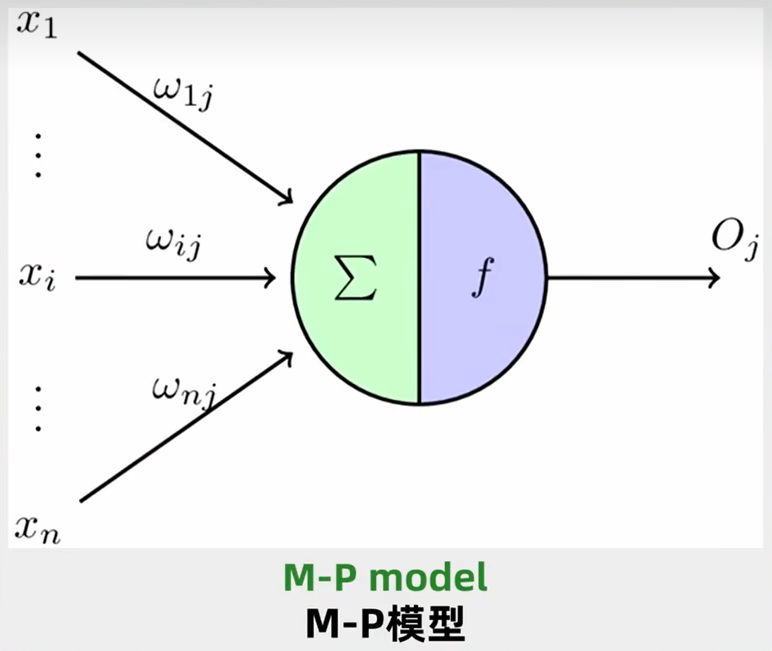
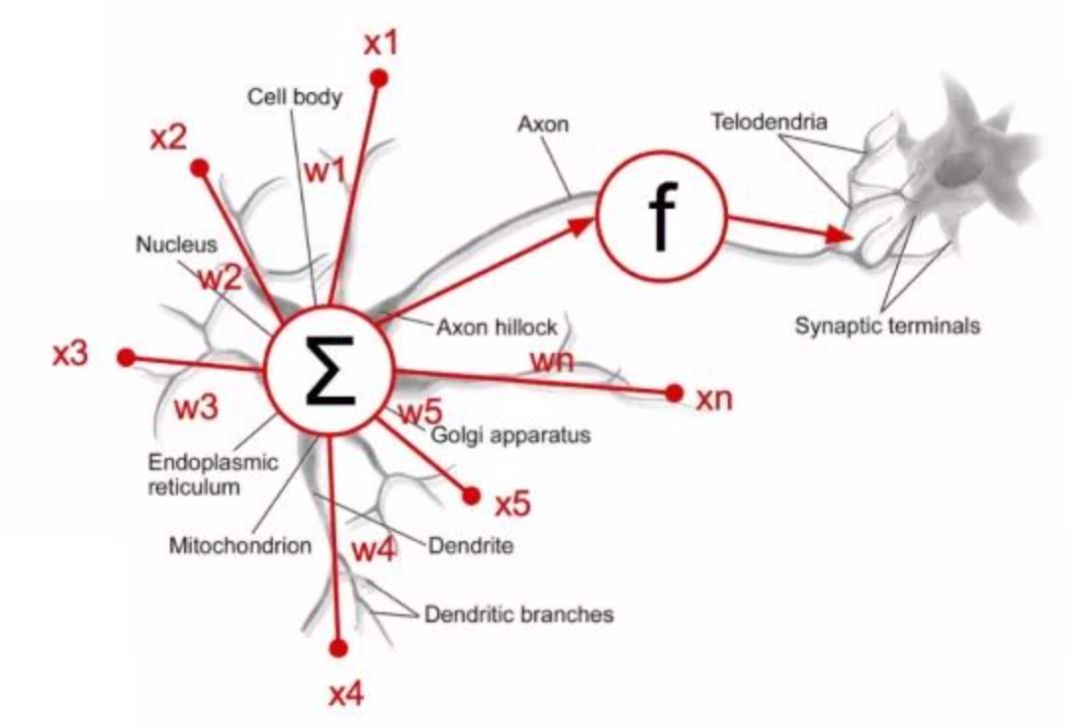
**如果我们把神经元模型化，就会得到一个 MP 模型。**如下图所示：

  • 小圆圈代表上一层神经元，大圆圈代表下一层神经元；
  • 小圆圈神经元会收到来自其他神经元的输入信号 x1x_1、x2x_2...一直到 xnx_n；
  • 每个小圆圈神经元包含了权重 w1w_1、w2w_2...一直到 wnw_n，它控制了各个输入信号的重要性；
  • 大圆圈神经元包含了偏置 bb ，它控制了神经元被激活的容易程度；

QQ截图20230808000307

我们将上面的模型用公式表达出来如下：

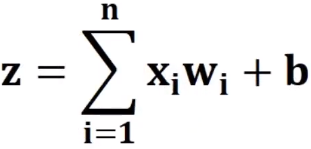
QQ截图20230809001411

  • 左侧是一堆输入信号 x1x_1、x2x_2...一直到 xnx_n；
  • 接着乘以一堆参数（权重） w1w_1、w2w_2...一直到 wnw_n；
  • 通过 ∑\sum 进行求和再加上一个 bb 偏置，得到一个 zz 结果；
  • 通过 ff 激活函数对 zz 结果进行处理，选择是否将这个数向下输出。

QQ截图20230613171503

img

激活函数 ​

**上面提到的”激活函数“，也叫“激励函数”，是运行在神经元上的数学函数，它负责将神经元上的线性累加值转换为非线性的输出，目的就是通过函数优化加速上面的纯线性计算过程。**激活函数有很多种，下面例举一些比较常用的激活函数：

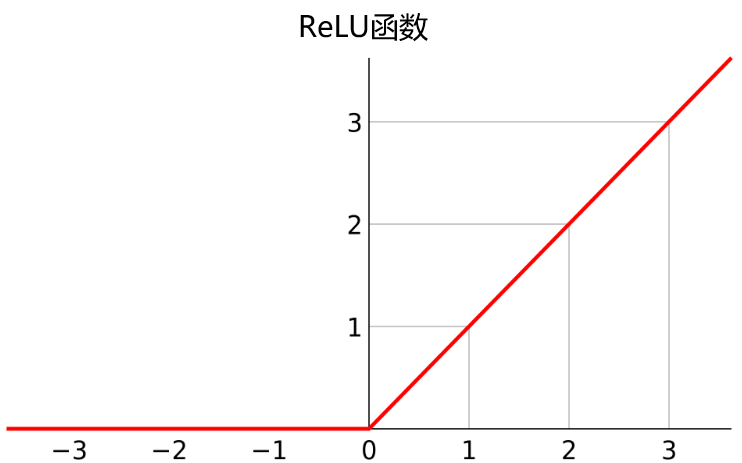
ReLU函数 ​

ReLU 函数结构简单，可以提高神经网络的整体计算效率，因此它也是最常用的线性激活函数。

f(x)=max(0,x)f(x) = max(0, x)

  • 若 xx 值小于或等于0时，f(x)f(x) 的值就是0；
  • 若 xx 值大于0时，f(x)f(x) 的值就是 xx 值；

QQ截图20230812024652

提醒

当输入大于1时，ReLU函数的梯度值恒为1，这就使得使用ReLU的神经元，在一定程度上可以缓解梯度消失问题。但在输入小于0时，ReLU函数恒为0，这会导致只要输入小于0，神经元就无法学习，这种现象被称为“死亡ReLU”。为了解决这个问题，可以使用变体的Leaky ReLU函数，即 f(x)=max(0.01x,x)f(x) = max(0.01x, x)，当输入值小于0时，函数输出0.01倍的输入值，这样即使输入值为负，神经元仍然有微小的梯度，不会完全“死亡”。

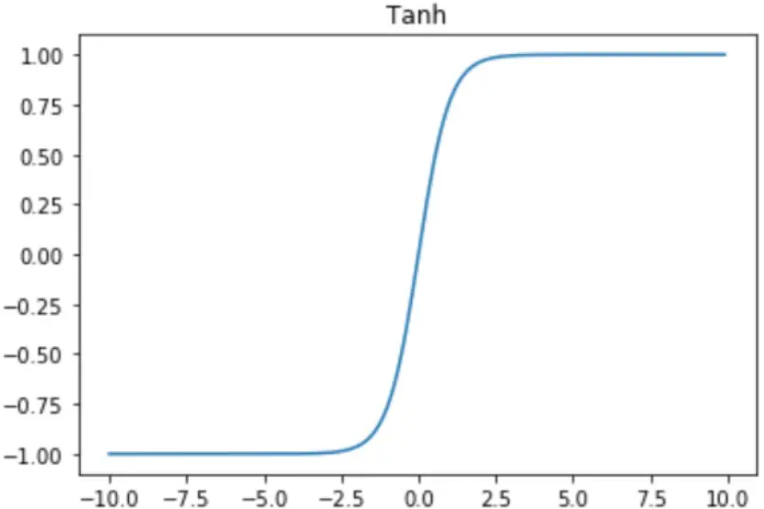
tanh函数 ​

tanh函数内容和特点如下：

f(x)=ex−e−xex+e−xf(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}}

QQ截图20230812025540

Sigmoid函数 ​

Sigmoid 函数内容和特点如下：

f(x)=11+e−xf(x) = \frac{1}{1+e^{-x}}

  • 当 xx 值越小时，f(x)f(x) 的值就趋近于0，也就是向下层输出的可能性也就越小；
  • 当 x=0x=0 时，f(x)f(x) 的值为0.5，也就是向下层输出的可能性为50%；
  • 当 xx 值越大时，f(x)f(x) 的值就趋近于1，也就是向下层输出的可能性也就越大；

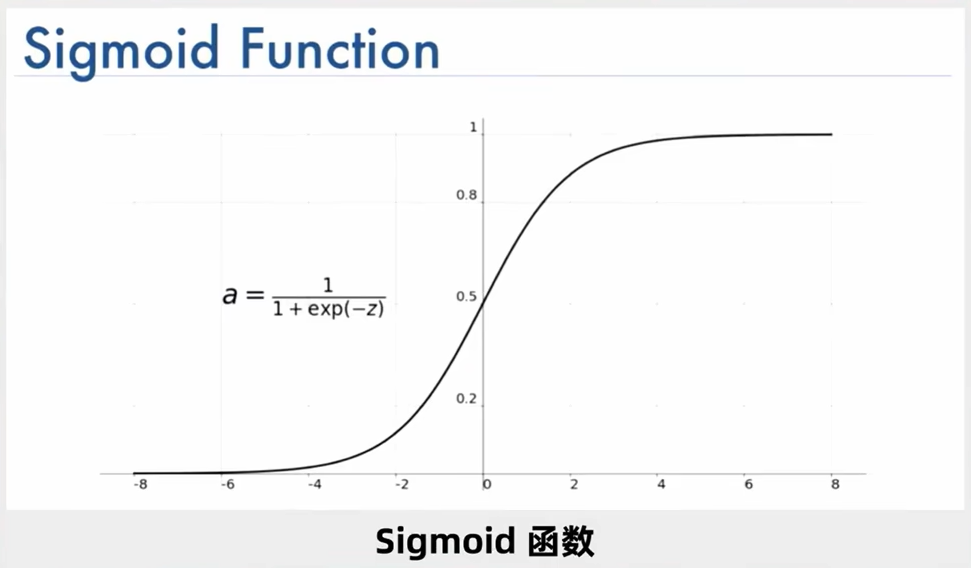
QQ截图20230613173632

选择Sigmoid函数作为激活函数，结合上面的神经元的计算步骤进入如下计算：

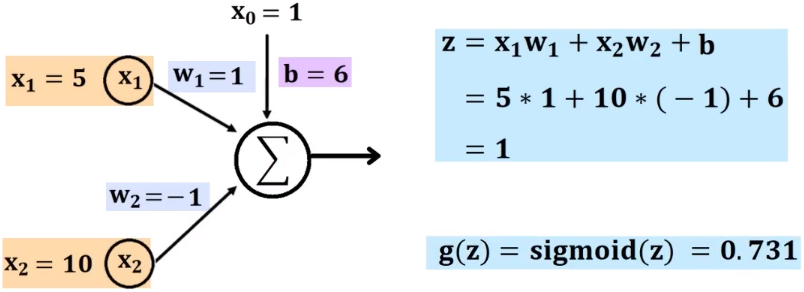
QQ截图20230812030629

建议

在生活我们识别物体其实也和激活函数一样，比如你看到一个动物，你认为它可能是个猫，也可能是个狗，再多看一会，你就有99%的可能性说它是狗，因此即便是人类判断物体，它也是有一定可能性的，所就存在这样一个激活函数选择是否向下层输出。

神经网络图 ​

单层网络 ​

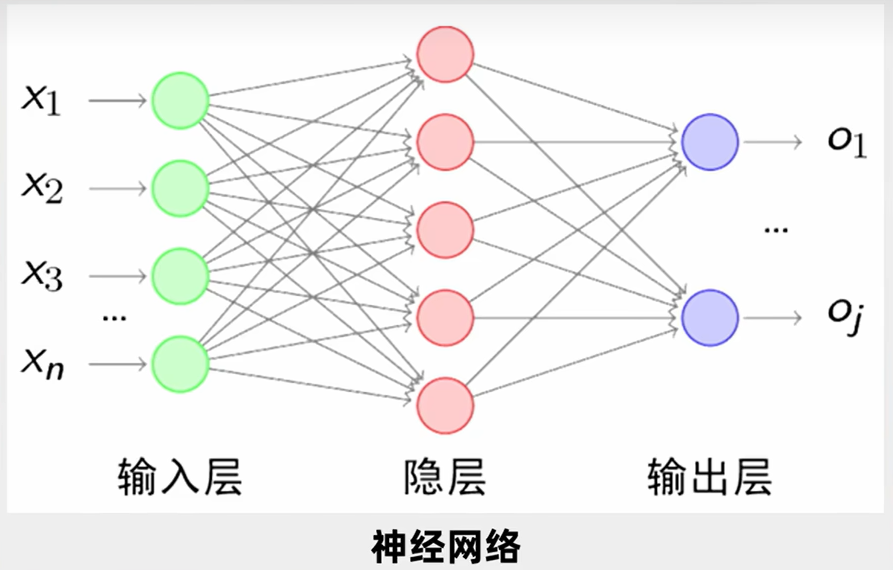
**神经网络肯定不止一个神经元，而是多个神经元的组合。**大家搜索神经网络时，可能看到过这样一张图，一些小圆圈，每两层之间的小圆圈都有连接，这其实就是一个神经网络图，它其实就是来源于人类对于大脑神经元的认知。如下图所示：

  • 每一个绿色圆圈、红色圆圈、紫色圆圈都是一个神经元；
  • 整体绿色圆圈代表“输入层”，它负责接收一大堆的自变量，比如 x1x_1、x2x_2...一直到 xnx_n；
  • 整体红色圆圈代表“隐层”，它负责判断处理，这一层我们通常是不关注的，因此也被称之为“隐层”；
  • 整体紫色圆圈代表“输出层”，它负责输出结果；

QQ截图20230613162046

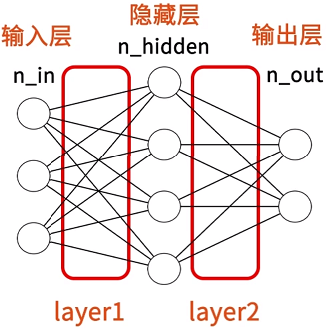
**除了上面讲到的层外，在神经网络中还有一种叫全连接层（线性层）。对于简单且样本数量足够多的数据集而言，单单一个全连接层就能达到一个不错的效果。**下图就是全连接层的展示：3个输入经过一次全连接层收敛为4个分类，再经历过一次全连接层收敛为2个分类。

QQ截图20230814173249

建议

有人肯定会有疑问，神经元明明是一个多输入单输出模型，然而“隐层”中的每个圆圈都有给“输出层”的每个圆圈输出。实际上“隐层”中的每个圆圈只有一个输出结果，它把这一个输出结果分别给到“输出层”的每个圆圈。

多层网络 ​

前面的线性回归可以看做是单层神经网络，但在现实生活中，如果要阅读文章要理解别人的语音，要进行图像识别，仅仅用一层神经网络是达不到效果的，于是就设计了多层神经网络，意思就是说你先有一个输入，然后输入端的连接每一个第一个隐层的神经元，然后第一个隐层把这些数据输出出来后，选择向下层输出，输出到第二隐层，第二隐层输出的结果又进入到第三隐层，这就是所谓的多层神经网络，每两层神经网络之间的链接都会有大量的参数，那么我们通过一定的算法，能够让大量的参数调节到最优，使得最后的误差函数最小，这样就是一个成功的训练。

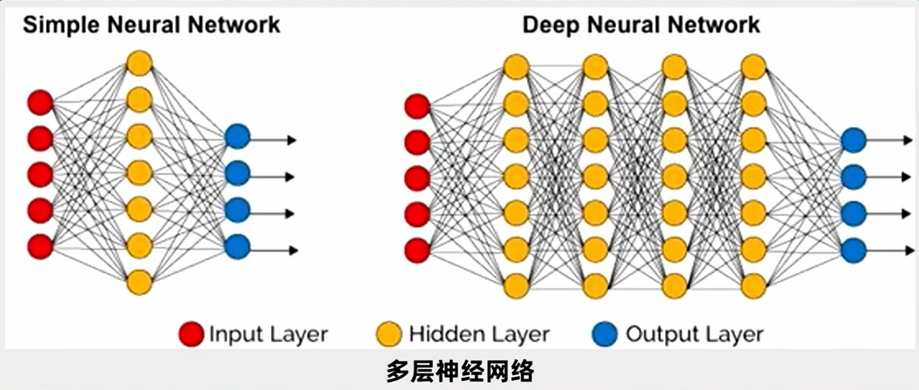
QQ截图20230613181547

建议

使用三层神经网络训练5X5大小的图片，每一层有25个神经元，每一层的参数就有600多个，三层就有2000来个参数需要调，而且这还是最简单图片，如果是一个彩色图，而且图片像素是1920X1080，那么识别起来就会非常复杂，算起来也会非常慢，这也是前几次人工智能陷入低谷的原因，就是不管是算力还是算法都跟不上，但现在都不用担心了。

优化器 ​

**优化器（optimizers）是神经网络中的重要组成部分，用于在训练神经网络时调整权重，使损失函数最小化。不同的优化器算法通常针对不同的目标，其使用方法也不同，如果同一个模型，选择不同的优化器，性能有可能相差很大，甚至导致一些模型无法训练。**一般情况下，优化器都需要以下几个超参数：

  • 学习率：用于控制权重在训练期间的更新速度，调整学习率可以影响优化器的收敛速度与质量。
  • 动量：用于控制权重的更新方向，使其更加稳定，一般用于处理局部最优解的情况。
  • 批量大小：用于控制权重的更新次数，影响每次批量更新的样本数量和权重调整速度。

传统下降 ​

在前面我们讲过梯度下降算法的三种形式，批量梯度下降算法（BGD）、随机梯度下降算法（SGD）、小批量梯度下降算法（MBGD）。这三个优化算法在训练的时候虽然所采用的数据量不同，但他们在进行参数优化时是相同的，在此把这三种算法统称为”传统梯度下降算法“，其基本思想是：**假设需要更新的参数为 θ\theta，梯度为 gg，设定一个学习率 λ\lambda，参数沿梯度的反方向移动。**则其更新策略可表示为：

θ←θ−λg\theta\leftarrow\theta-\lambda{g}

在 PyTorch 中，传统的梯度下降算法可以使用 torch.optim.SGD 格式：

python
# params模型参数、lr学习率、momentum动量
torch.optim.SGD(params, lr=<required parameter>, momentum=0, dampening=0, weight_decay=0, nesterov=False, *, maximize=False)

**使用传统的梯度下降算法，一般只设置模型参数、学习率，其他参数默认即可。**下面看一看它的用法：

python
import torch

# 优化器，传统梯度下降算法
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
# 计算loss值，对模型参数求偏导
loss_fn(model(input), target).backward()
# 参数更新
optimizer.step()
# 梯度清零
optimizer.zero_grad()

虽然传统梯度更新算法十分简洁，当学习率取值恰当时，可以收敛到全面最优点(凸函数)或局部最优点(非凸函数)。但其还有很大的不足点：

  1. 对学习率敏感，过小导致收敛速度过慢，过大又越过极值点；
  2. 有时会因其在迭代过程中保持不变，容易造成算法被卡在一个不是局部最小值的驻点（一阶导数为0的点）；
  3. 在较平坦的区域，由于梯度接近于0，优化算法会误判，在还未到达极值点时，就提前结束迭代，陷入局部极小值。

针对传统梯度优化算法的缺点，许多优化算法从**“梯度方向”和“学习率”两方面入手。有些从梯度方向入手，如“动量更新策略”；而有些从学习率入手，这涉及调参问题；还有从两方面同时入手，如“自适应梯度下降”**。

自适应下降 ​

**Adam（Adaptive Moment Estimation）是一种比SGD更为先进的优化器算法，该算法不仅可以自适应调节学习率，还可以调整动量，使训练更稳定、更快速、更容易达到最优解，因此广泛应用在处理稀疏数据中，例如文本数据、图像数据。**在 PyTorch 中，使用自适应更新算法可以使用 torch.optim.Adam 格式：

python
# params模型参数、lr学习率、betas分别控制权重分配和之前的梯度平方的影响情况
torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False, *, maximize=False)

BP算法 ​

**BP 算法（Backpropagation）是神经网络训练的核心算法之一，它建立在梯度下降算法基础之上，使得神经网络能够学习复杂的非线性映射，并调整其参数以最小化损失函数，逐步提高对输入数据的预测或分类性能。**BP算法包括以下步骤：

  1. 正向传播（Forward Propagation）：

    • 输入数据通过神经网络的各个层，经过权重和激活函数的作用，得到模型的输出。
    • 正向传播的过程是从网络的输入开始，逐层计算每一层的输出，直到达到输出层。
    • 记录每一层的输入和输出，以备用于反向传播。

  2. 计算损失函数（Loss Calculation）：

    • 将网络输出与实际标签进行比较，计算损失函数，衡量模型的预测与真实值之间的差异。

  3. 反向传播（Backward Propagation）：

    • 计算损失函数对每个参数（权重和偏置）的梯度。
    • 从输出层开始，逐层反向传播梯度，计算每一层的梯度，使用链式法则。
    • 梯度表示了损失函数相对于每个参数的变化率。

  4. 参数更新（Parameter Update）：

    • 使用梯度下降或其他优化算法，根据损失函数的梯度更新网络的参数。
    • 重复以上步骤，通过多次迭代逐渐调整参数，降低损失函数。

  5. 重复训练（Repeat Training）：

    • 重复以上步骤直到损失函数足够小，或者达到预定义的停止条件。

建议

BP算法在调整参数的时候，不用像以前那样从前往后一层层调试，而是可以先调最后一层，最后一层调完以后，再往前调，一直调到最前面这一层。也正是由于反向传播算法比以前的算法复杂度要低，因此也引领了第三次人工智能浪潮。

拟合正弦函数 ​

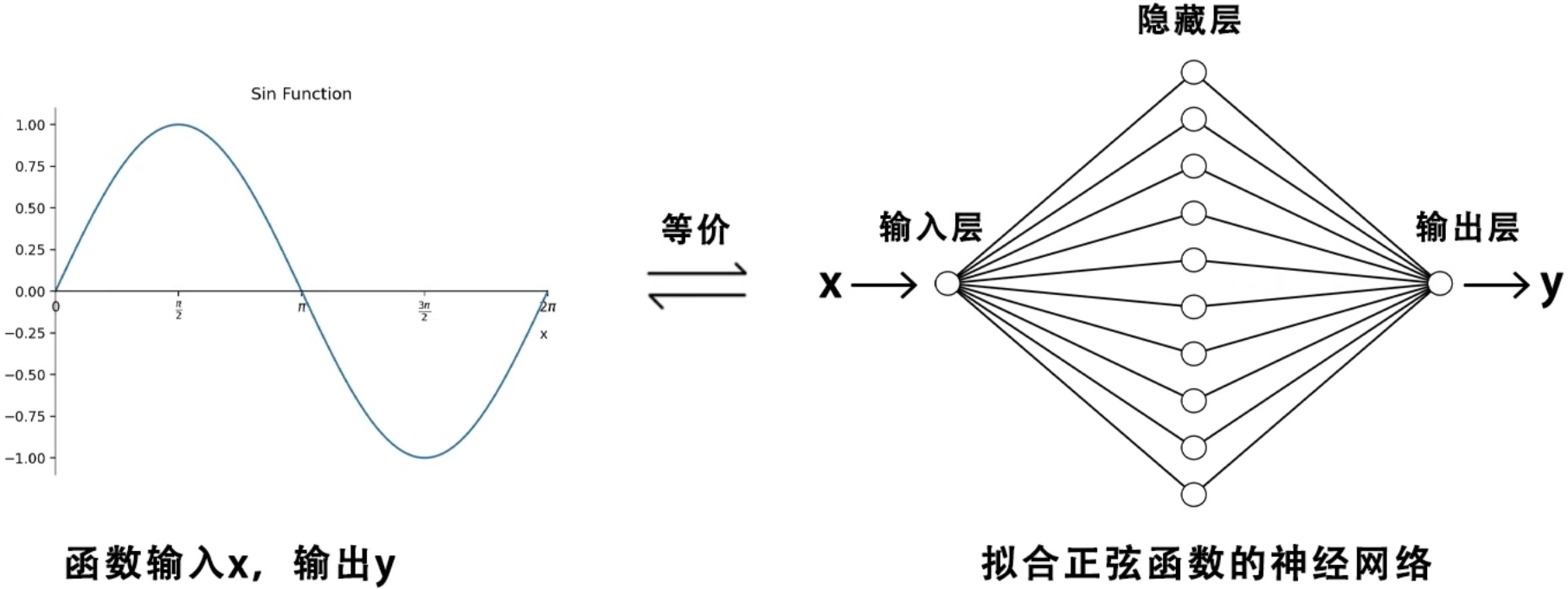
现在我们要基于 PyTorch 深度学习框架实现一个前馈神经网络模型，并训练这个神经网络，使它拟合出正弦函数。我们要训练一个三层神经网络，该网络具有正弦函数的功能，当向它输入 x 时，会输出与正弦函数相同的结果 y。具体来说，神经网络的输入层有 1 个神经元，负责接收 x 信号，隐藏层有 10 个神经元，负责生成模拟正弦函数的特征，输出层有 1 个神经元，输出正弦结果。

QQ截图20230812031735

定义模型 ​

**在 PyTorch 中 nn.Module 是最重要的类之一，它是构建神经网络等各类模型的基类。**我们可以将 nn.Module 看作是模型的框架，我们在实现自己的模型时，需要继承 nn.Module 类，并重新实现和覆盖其中的一些方法，其中包含两个重要的函数，分别是 init 和 forward 函数。

  • init 方法会在创建类的新实例时被自动调用，我们会在 init 方法中定义模型的层和参数，比如线性层、激活函数、卷积层等等。

  • forward 方法定义了输入数据如何通过模型，或者说模型如何计算输入数据，也就是神经网络在进行前向传播时的具体操作。

现在我们基于 nn.Module 模块，实现一个三层神经网络模型，代码如下：

python
import torch
from torch import nn

# 神经网络类Network，继承nn.Module类
class Network(nn.Module):
    # 数传入参数n_in, n_hidden, n_out分别代表输入层、隐藏层和输出层中的特征数量。
    def __init__(self, n_in, n_hidden, n_out):
        # 调用torch.nn.Module父类的初始化函数
        super().__init__()
        # layer1是输入层与隐藏层之间的线性层
        self.layer1 = nn.Linear(n_in, n_hidden)
        # layer2是隐藏层与输出层之间的线性层
        self.layer2 = nn.Linear(n_hidden, n_out)

    # 实现神经网络的前向传播，函数传入输入数据x
    def forward(self, x):
        x = self.layer1(x)  # 计算layer1的结果
        x = torch.sigmoid(x)  # 进行sigmoid激活
        return self.layer2(x)  # 计算layer2的结果，并返回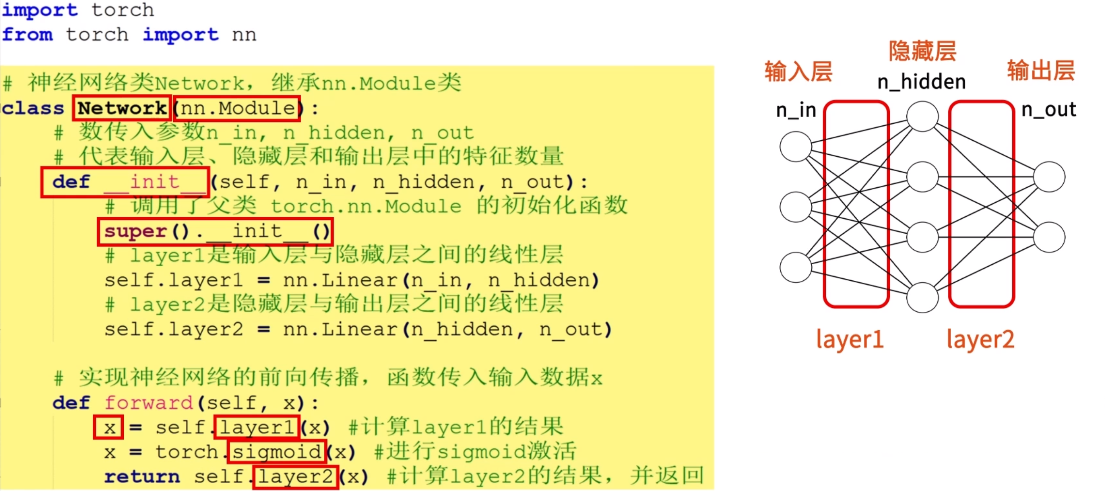

image-20231219180706245

生成数据 ​

python
from matplotlib import pyplot as plt
import numpy as np

if __name__ == '__main__':
    # 使用np.arrange生成一个从0到1，步长为0.01
    # 含有100个数据点的数组，作为正弦函数的输入数据
    x = np.arange(0.0, 1.0, 0.01)
    # 将0到1的x，乘以2π，从单位间隔转换为弧度值
    # 将x映射到正弦函数的一个完整周期上，并计算正弦值
    y = np.sin(2 * np.pi * x)
    # 将x和y通过reshape函数转为100乘1的数组
    # 也就是100个(x, y)坐标，代表100个训练数据
    x = x.reshape(100, 1)
    y = y.reshape(100, 1)
    # 将(x, y)组成的数据点，画在画板上
    plt.scatter(x, y)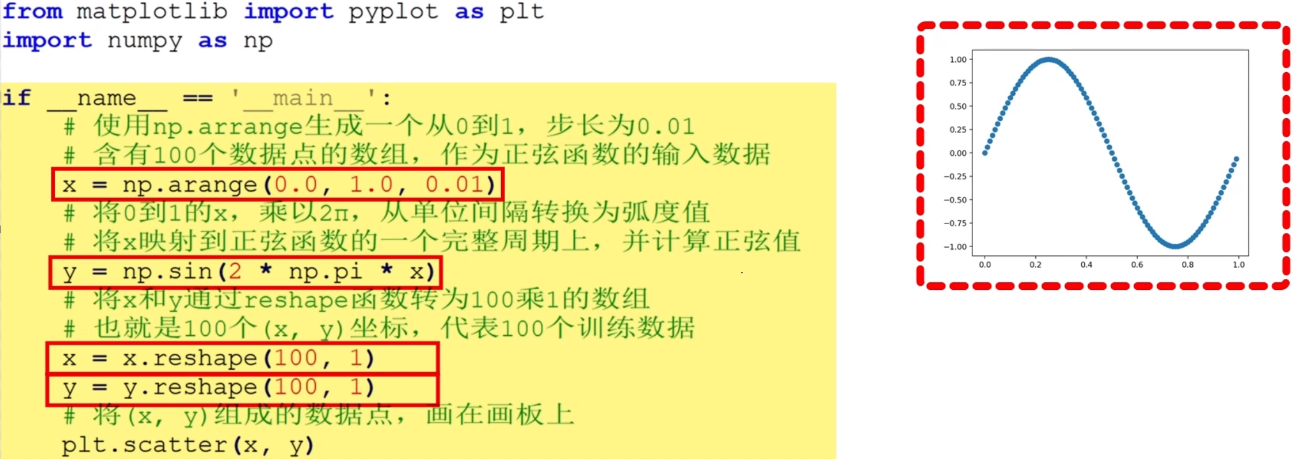

image-20231219180850849

模型迭代 ​

python
# 将x、y数据tensor张量
x = torch.Tensor(x)
y = torch.Tensor(y)
# 定义一个3层的神经网络model，(1, 10, 1)分别代表1个输入层神经元，10个隐藏层神经元，1个输出层神经元。
model = Network(1, 10, 1)
# 均方误差损失函数
criterion = nn.MSELoss()  
# Adam优化器optimizer
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)

for epoch in range(10000):  # 进入神经网络模型的循环迭代
    # 前向传播
    y_pred = model(x)  # 使用当前的模型，预测训练数据x
    # 反向传播
    loss = criterion(y_pred, y)  # 计算预测值y_pred与真实值y_tensor之间的损失
    loss.backward()  # 通过自动微分计算损失函数关于模型参数的梯度
    optimizer.step()  # 更新模型参数，使得损失函数减小
    optimizer.zero_grad()  # 将梯度清零，以便于下一次迭代
    # 模型的每一轮迭代，都由前向传播和反向传播共同组成
    if epoch % 1000 == 0:
        # 每1000次迭代，打印一次当前的损失
        print(f'After {epoch} iterations, the loss is {loss.item()}')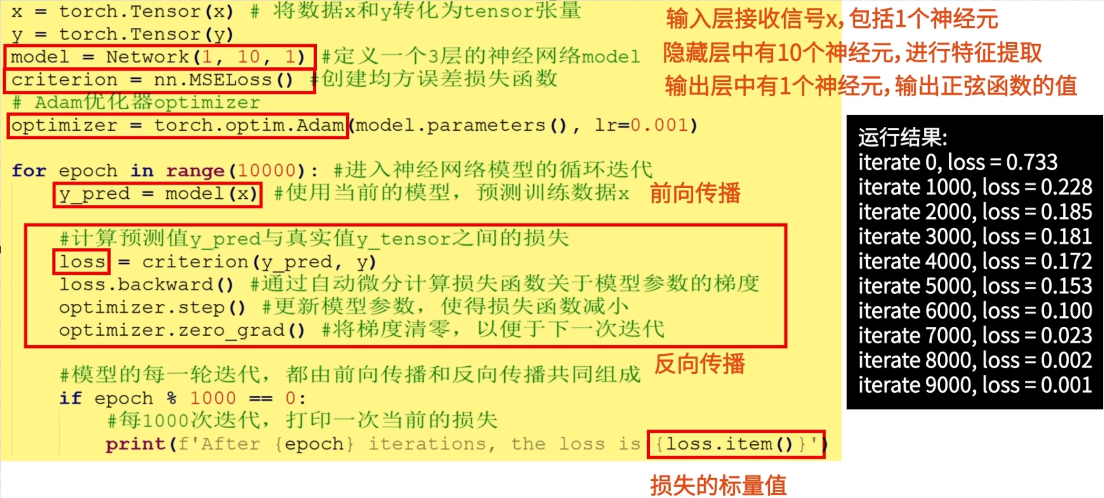

image-20231219181044896

结果可视化 ​

python
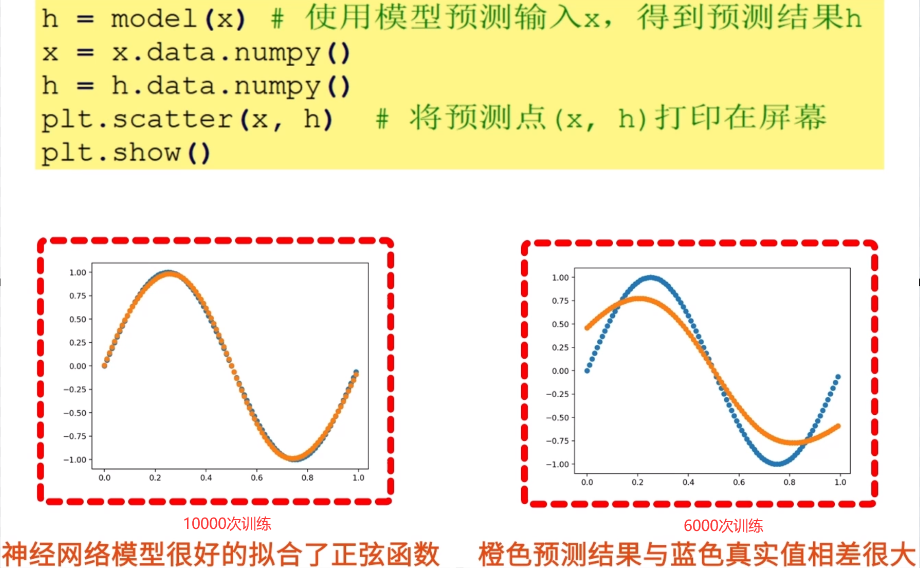
h = model(x)  # 使用模型预测输入x，得到预测结果h
x = x.data.numpy()
h = h.data.numpy()
plt.scatter(x, h)   # 将预测点(x, h)打印在屏幕
plt.show()

image-20231219181246661