如何计算数字

更新: 2025/2/24 字数: 0 字 时长: 0 分钟

数字编码

原码、反码和补码

所有整数类型能够表示的负数都比正数多一个，例如 byte 的取值范围是 [−128,127] 。这个现象比较反直觉，它的内在原因涉及原码、反码、补码的相关知识。

首先需要指出，数字是以“补码”的形式存储在计算机中的。在分析这样做的原因之前，首先给出三者的定义。

• 原码：我们将数字的二进制表示的最高位视为符号位，其中 $0$ 表示正数，$1$ 表示负数，其余位表示数字的值。
• 反码：正数的反码与其原码相同，负数的反码是对其原码除符号位外的所有位取反。
• 补码：正数的补码与其原码相同，负数的补码是在其反码的基础上加 $1$ 。

下图展示了原码、反码和补码之间的转换方法。

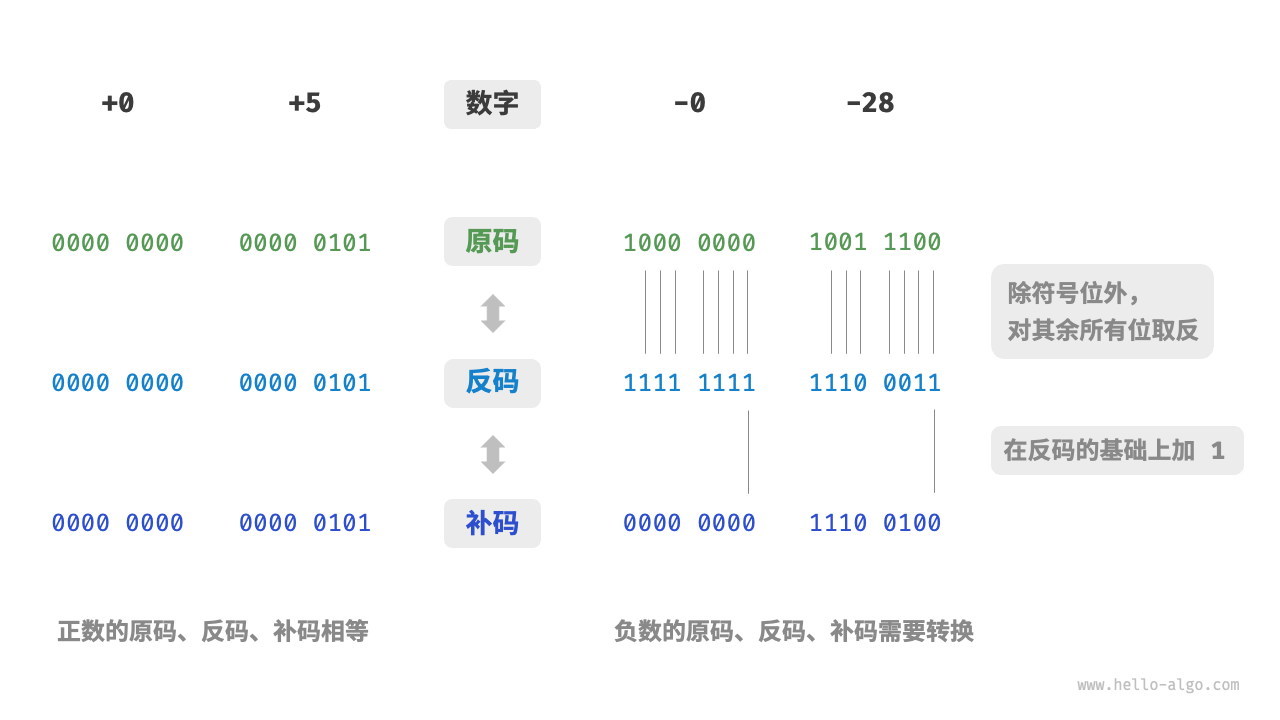
原码（sign-magnitude）虽然最直观，但存在一些局限性。一方面，负数的原码不能直接用于运算。例如在原码下计算 1+(−2) ，得到的结果是 −3 ，这显然是不对的。

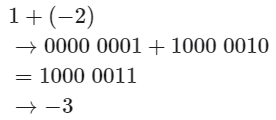
为了解决此问题，计算机引入了反码（1's complement）。如果我们先将原码转换为反码，并在反码下计算 1+(−2) ，最后将结果从反码转换回原码，则可得到正确结果 −1 。

另一方面，数字零的原码有 $+0$ 和 $-0$ 两种表示方式。这意味着数字零对应两个不同的二进制编码，这可能会带来歧义。比如在条件判断中，如果没有区分正零和负零，则可能会导致判断结果出错。而如果我们想处理正零和负零歧义，则需要引入额外的判断操作，这可能会降低计算机的运算效率。

与原码一样，反码也存在正负零歧义问题，因此计算机进一步引入了补码（2's complement）。我们先来观察一下负零的原码、反码、补码的转换过程：

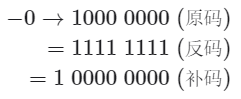
在负零的反码基础上加 $1$ 会产生进位，但 byte 类型的长度只有 8 位，因此溢出到第 9 位的 $1$ 会被舍弃。也就是说，负零的补码为 $00000000$ ，与正零的补码相同。这意味着在补码表示中只存在一个零，正负零歧义从而得到解决。

还剩最后一个疑惑：byte 类型的取值范围是 [−128,127] ，多出来的一个负数 $-128$ 是如何得到的呢？我们注意到，区间 [−127,+127] 内的所有整数都有对应的原码、反码和补码，并且原码和补码之间可以互相转换。

然而，补码 $10000000$ 是一个例外，它并没有对应的原码。根据转换方法，我们得到该补码的原码为 $00000000$ 。这显然是矛盾的，因为该原码表示数字 $0$ ，它的补码应该是自身。计算机规定这个特殊的补码 $10000000$ 代表 $-128$ 。实际上，$(-1)+(-127)$ 在补码下的计算结果就是 $-128$ 。

浮点数编码

细心的你可能会发现：int 和 float 长度相同，都是 4 字节 ，但为什么 float 的取值范围远大于 int ？这非常反直觉，因为按理说 float 需要表示小数，取值范围应该变小才对。

实际上，这是因为浮点数 float 采用了不同的表示方式。记一个 32 比特长度的二进制数为：

根据 IEEE 754 标准，32-bit 长度的 float 由以下三个部分构成。

• 符号位 $S$ ：占 1 位 ，对应 $b_{31}$ 。
• 指数位 $E$ ：占 8 位 ，对应 $b_{30}b_{29}...b_{23}$ 。
• 分数位 $N$ ：占 23 位 ，对应 $b_{22}b_{21}...b_{0}$ 。

二进制数 float 对应值的计算方法为：

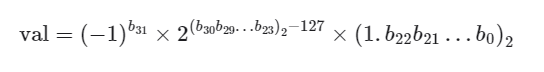
转化到十进制下的计算公式为：

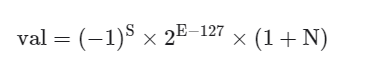
其中各项的取值范围为：

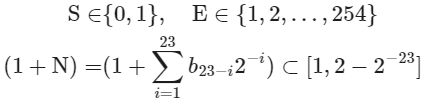
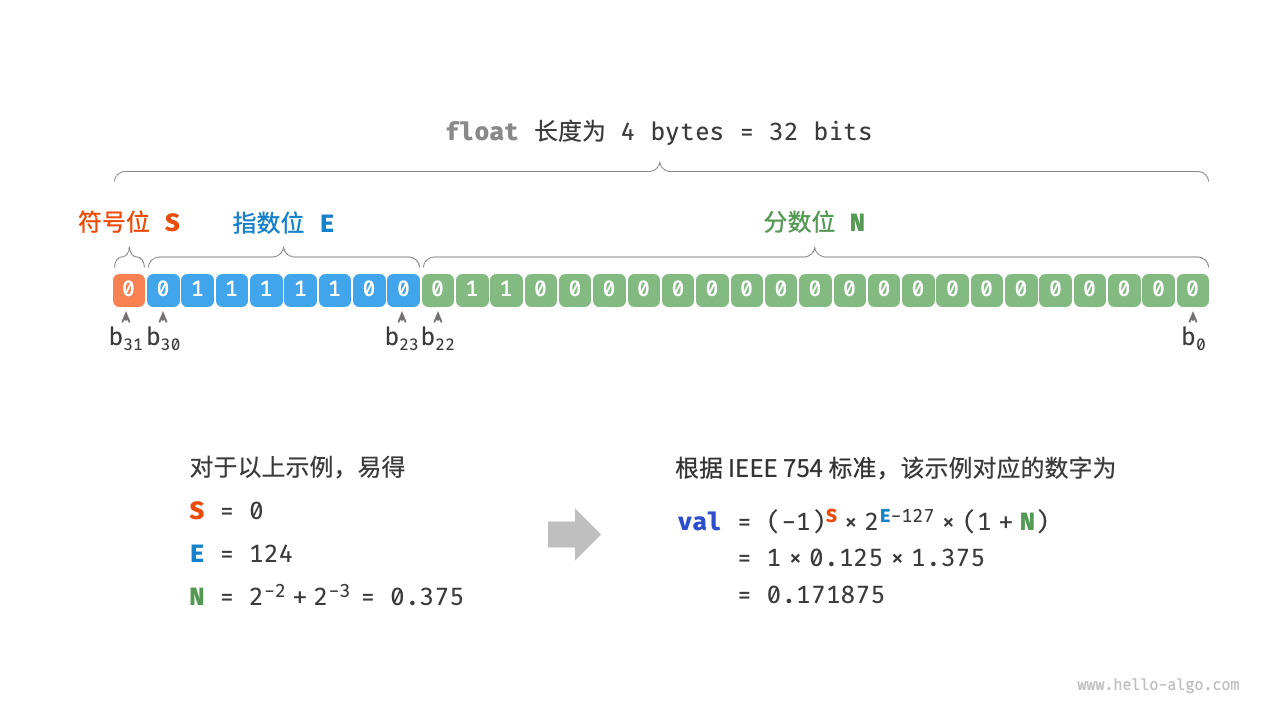
观察上图，给定一个示例数据 $S=0$ ， $E=124$ ，$N=2^{-2}+2^{-3}=0.375$ ，则有：

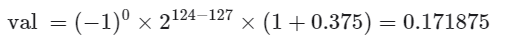
现在我们可以回答最初的问题：float 的表示方式包含指数位，导致其取值范围远大于 int 。根据以上计算，float 可表示的最大正数为 $2^{254-127}\times(2-2^{-23})\approx3.4\times10^{38}$ ，切换符号位便可得到最小负数。

尽管浮点数 float 扩展了取值范围，但其副作用是牺牲了精度。整数类型 int 将全部 32 比特用于表示数字，数字是均匀分布的；而由于指数位的存在，浮点数 float 的数值越大，相邻两个数字之间的差值就会趋向越大。

如下表所示，指数位 $E=0$ 和 $E=255$ 具有特殊含义，用于表示零、无穷大、$NaN$ 等。

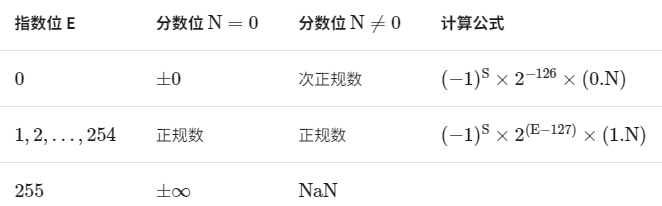
值得说明的是，次正规数显著提升了浮点数的精度。最小正正规数为 $2^{-126}$ ，最小正次正规数为 $2^{-126}\times2^{-23}$ 。

双精度 double 也采用类似于 float 的表示方法，在此不做赘述。

Q&A

Q：原码转补码的方法是“先取反后加 1”，那么补码转原码应该是逆运算“先减 1 后取反”，而补码转原码也一样可以通过“先取反后加 1”得到，这是为什么呢？

A：这是因为原码和补码的相互转换实际上是计算“补数”的过程。我们先给出补数的定义：假设 $a+b=c$ ，那么我们称 $a$ 是 $b$ 到 $c$ 的补数，反之也称 $b$ 是 $a$ 到 $c$ 的补数。

给定一个 $n=4$ 位长度的二进制数 $0010$ ，如果将这个数字看作原码（不考虑符号位），那么它的补码需通过“先取反后加 $1$”得到：

我们会发现，原码和补码的和是 $0010+1110=10000$ ，也就是说，补码 $1110$ 是原码 $0010$ 到 $10000$ 的“补数”。这意味着上述“先取反后加 $1$”实际上是计算到 $10000$ 的补数的过程。

那么，补码 $1110$ 到 $10000$ 的“补数”是多少呢？我们依然可以用“先取反后加 $1$”得到它：

换句话说，原码和补码互为对方到 $10000$ 的“补数”，因此“原码转补码”和“补码转原码”可以用相同的操作（先取反后加 $1$ ）实现。当然，我们也可以用逆运算来求补码 $1110$ 的原码，即“先减 $1$ 后取反”：

总结来看，“先取反后加 $1$”和“先减 $1$ 后取反”这两种运算都是在计算到 $10000$ 的补数，它们是等价的。

本质上看，“取反”操作实际上是求到 $1111$ 的补数（因为恒有 原码 + 反码 = 1111）；而在反码基础上再加 $1$ 得到的补码，就是到 $10000$ 的补数。

上述 $n=4$ 为例，其可推广至任意位数的二进制数。