剑眉星目

深浅模式

线性回归 ​

更新: 2025/2/24 字数: 0 字 时长: 0 分钟

线性回归（Linear Regression）是指通过一条线近似的表示自变量和因变量之间的关系，用于对一个或多个自变量和因变量之间的关系进行建模。在模型中包含了几个自变量，就是几元的线性回归。

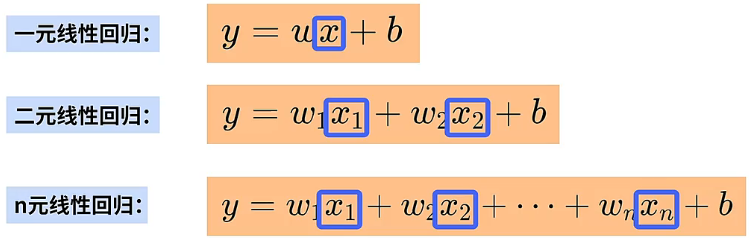
image-20241028232320585

提醒

线性回归是机器学习中最基础的一个模型，也是我们理解后面所有深度模型的基础。

房价预测 ​

在现实生活中，很多问题都可以使用线性回归来表示，这里我们以预测房价为例来说明线性回归。

一元回归模型 ​

在实际生活中，一个房子的房价受地段、面积、楼层、小区等一系列变量的影响，这里为了方便理解，先简化一下变量，就简单认为房屋价格只取决于房屋面积，即面积越大价格越高，那么此时价格就是关于面积的一元函数：

image-20240913222829007

既然价格是关于面积的一元函数，我们就可以使用一元线性回归方程（一元回归模型）来描述面积和价格之间的关系，具体如下：

image-20241027002447073

  • xx 是自变量，代表房屋的面积，同时也是模型的输入。
  • yy 是因变量，代表房屋的预测价格，同时也是模型的输出。
  • ww 和 bb 是我们需要计算出来的常量值，同是也是模型的参数。

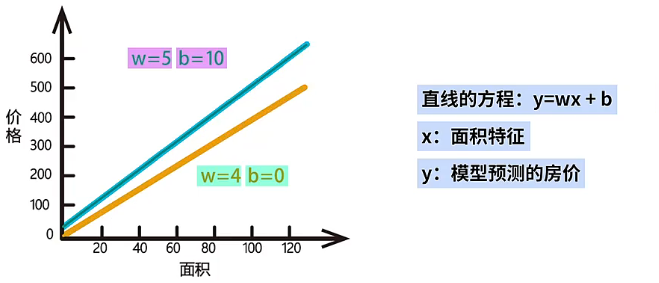
现在我们将回归模型在坐标系中画出来，其中横坐标 xx 表示面积，纵坐标 yy 表示价格，具体如下：当 ww 和 bb 取不同的值时，会得到不同的直线，使用不同的直线基于面积预测价格的效果也是不同的。

image-20241030233530414

数据样本表示 ​

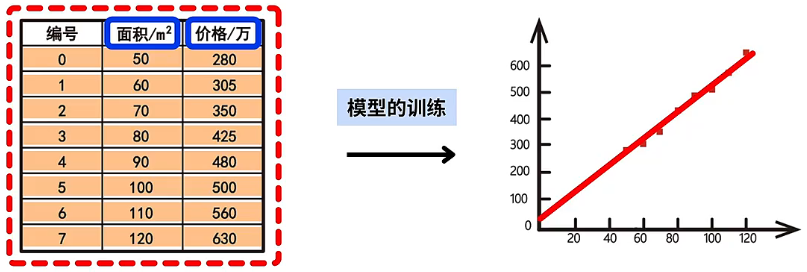
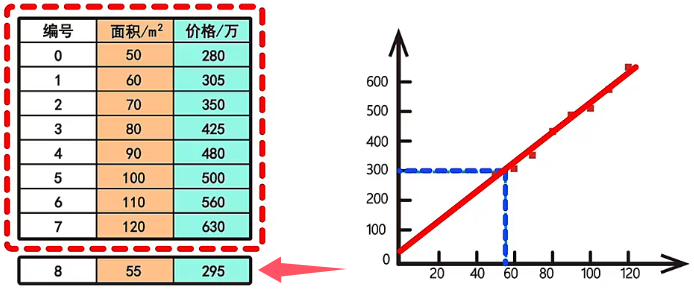
确定好了回归模型以后，就要准备训练模型所用的数据了。我们将所有用来训练模型的数据统称为“数据集”，其中用于训练模型的数据集被称为“训练集”。例如，下面房屋面积和房屋价格的数据表格就是一个训练集：

编号（ii）面积/平方米（xx）价格/万（yy）
050208
160305
270350
380425
490480
5100500
6110560
7120630
  • 编号：代表的是样本编号，使用 ii 表示。通常情况下，我们不会将样本编号表示在训练集中，即使一份数据包含了样本编号这一列，这一列也不会用作训练，它的作用只是方便人们观看样本。
  • 面积/平方米：代表的是自变量，同时也是训练模型时，所用到的输入特征，使用 xx 表示。
  • 价格/万：代表的是因变量，训练集中的价格一般是人们手工标记或者刻意收集的，使用 yy 表示，使用 y^\hat{y} 或 hh 表示模型对于因变量的预测值。

现在我们将这三个变量组合为 (x(i),y(i))(x^{(i)},y^{(i)}) 的形式来表示一个训练样本，其中 ii 代表样本编号，xx 代表自变量房屋面积，yy 代表因变量房屋价格。例如，上面表格中编号为 33 的样本是 (80,425)(80,425) 记作 (x(3),y(3))(x^{(3)},y^{(3)})。另外，由于该例子中只有一个输入特征（面积），因此直接使用 xx 表示这个特征就可以了，但如果有多个输入特征，可以使用 xx 加下角标的方式表示特征的编号，例如使用 x1x_1 表示面积、 x2x_2 表示位置、 x3x_3 表示楼层等等，这就是多元线性回归的特征表示方法。在下面图中。上角标表示了第几个样本，下角标表示了第几个特征：

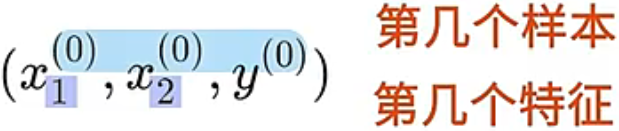
image-20241104192446647

除了上述的三个变量以外，还有一个表示样本数量的变量，使用 mm 表示。例如，上述训练集中有 8 组数据，那么变量 m=8m=8，同时样本编号 ii 的取值范围如下：

i∈{0,1,2,...,m−1}i\in\{0,1,2,...,m-1\}

模型训练过程 ​

训练集准备好后，我们将基于训练集对回归模型进行训练。为了更明显的观察面积和价格之间的关系，我们建立一个坐标系，其中横坐标表示面积 xx，纵坐标表示价格 yy，将训练集中的八组数据以点的形式标记在坐标系中，具体如下：

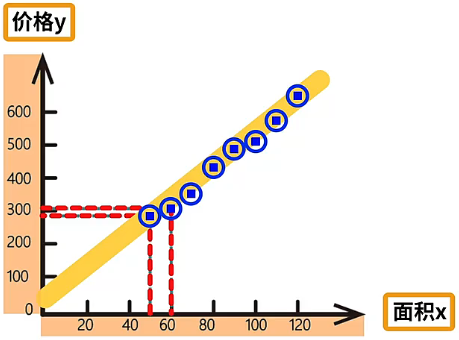
image-20241027011524084

整体观察就能发现，这些离散的数据点之间存在着近似的线性关系，而一元线性回归模型也是一条直线，那么接下来就是要寻找一条与所有数据点重合度最高的直线（即找到描述面积和价格之间关系的最佳模型），这就是一元线性回归模型的训练过程。

image-20241028224229492

提醒

需要说明的是，上面说寻找“重合度最高的直线”，为什么不能是“完全重合的直线”呢？因为每组数据中房价和面积的关系不一定能同时满足同一个函数，因此一条直线可能不会同时符合所有的数据，甚至可能一组数据都不符合。

损失函数量化 ​

那么如何找出最合适的模型参数 ww 和 bb，使得模型能够准确的描述面积和价格的关系呢？有的小伙伴可能会回答说，我们可以手动调整模型参数 ww 和 bb，具体情况如下：

  • 当 w=4w=4、b=0b=0 时，可以看到模型直线的斜率和截距都是偏小。
  • 当 w=5w=5、b=10b=10 时，可以看到模型直线基本符合了面积和价格的关系。

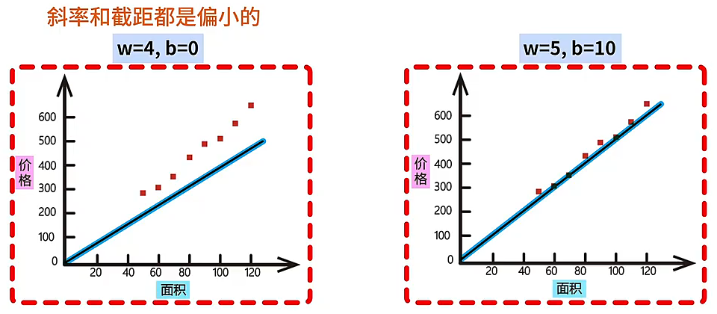
image-20241107000301964

在调整模型参数 ww 和 bb 的过程中，我们会发现直线的变化越来越小，很难观察出哪条直线最符合面积和房价的关系，例如下面三条直线：它们的参数 ww 和 bb 的差距很小，但具体哪条直线最好，是没办法通过观察来确定的。

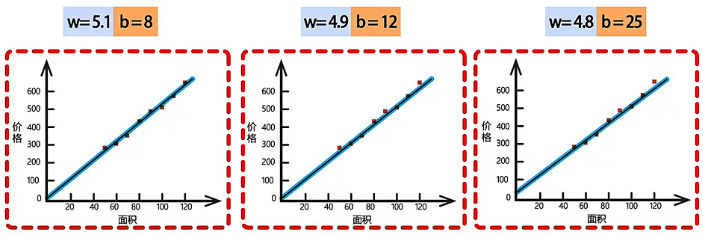
image-20241107000814875

这种情况下，就需要一个函数来量化计算出单个数据样本中模型预测值与训练真实值之间的误差，我们称这类函数为损失函数（Loss Function）。损失函数所量化计算出的误差就是损失值（Loss Value），损失值越小，则说明预测值和真实值之间误差就越小。那么如何量化计算误差呢？很简单，第一个房子实际价格 y1y_1 高于模型预测价格 y1^\hat{y_1}，两个价格之间的差值就为 y1−y1^y_1-\hat{y_1}（正误差），第二个房子实际价格 y2y_2 低于模型预测价格 y2^\hat{y_2}，两个价格之间的差值就为 y2−y2^y_2-\hat{y_2}（负误差），以此类推我们就能得到所有的误差，具体表现为如下图：

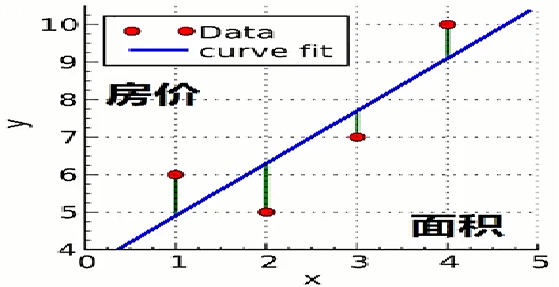
image-20241108000605553

(y1−y1^),(y2−y2^),...,(yn−yn^)(y_1-\hat{y_1}),(y_2-\hat{y_2}),...,(y_n-\hat{y_n})

当所有误差都计算出来了以后，如果直接相加的话，正负误差会相互抵消，所以需要通过一定的方法对误差进行处理，以消除这种抵消。最常的两种方法就是绝对值或者算术平方，因此这里就对应如下两种损失函数（yy 是真实值，y^\hat{y} 是预测值）：

  • 绝对损失函数，计算单个样本的预测值和真实值之间误差的绝对值。

L(y,y^)=∣y−y^∣L(y,\hat{y})=|y-\hat{y}|

  • 平方损失函数，计算单个样本的预测值和真实值之间误差的算术平方。

L(y,y^)=(y−y^)2L(y,\hat{y})=(y-\hat{y})^2

建议

损失函数不仅包括上面介绍到的两种，还包括 log 对数损失函数、0-1 损失函数（zero-one loss）、指数损失函数（exponential loss）、感知损失函数（perceptron loss）等，每一种损失函数都对应一种数学模型计算。在具体的项目中，损失函数的选择十分关键，选择合适的损失函数，可以加快模型的训练速度。

代价函数度量 ​

损失函数计算的是某一个样本的误差，但一个样本的误差大小不足以反应整个数据集的损失，因此我们还需要使用代价函数（Cost Function）来度量整个数据集上的平均损失。具体怎么做呢？很简单，将所有样本的损失值求和以后，除以样本数量就得到一个平均损失。上面介绍了两种损失函数，这里就介绍对应的两种代价函数（mm 是样本数量，y(i)y^{(i)} 和 y^(i)\hat{y}^{(i)} 分别是第 ii 个样本的真实值和预测值）：

  • 绝对误差（Mean Absolute Error，MAE），也叫绝对损失或 L1 loss，计算所有样本损失值的绝对值求和以后的平均值。
\begin{aligned} MAE&=\frac{1}{m}(|y_1-\hat{y_1}|+|y_2-\hat{y_2}|+...+|y_m-\hat{y_m}|)\\ MAE&=\frac{1}{m}\sum_{i=1}^{m}|y_i-\widehat y_i|\\ \end{aligned}
python
import torch
import torch.nn as nn

# L1Loss函数
loss_f = nn.L1Loss()
one = torch.Tensor([2, 3, 4, 5])
two = torch.Tensor([4, 5, 6, 7])
print(loss_f(one, two))  # 输出：tensor(2.)。注释：(|2-4|+|3-5|+|4-6|+|5-7|)/4=2。
  • 均方误差（Mean Squared Error，MSE），也叫平方损失或 L2 loss，计算所有样本损失值的平方值求和以后的平均值。
\begin{aligned} MSE&=\frac{1}{m}[(y_1-\hat{y_1})^2+(y_2-\hat{y_2})^2+...+(y_m-\hat{y_m})^2]\\ MSE&=\frac{1}{m}\sum_{i=1}^{m}(y_i-\widehat y_i)^2\\ \end{aligned}
python
import torch
import torch.nn as nn

# 均方误差MSE
loss_f = nn.MSELoss()
one = torch.Tensor([2, 3, 4, 5])
two = torch.Tensor([4, 5, 6, 7])
print(loss_f(one, two))  # 输出：tensor(4.)。注释：((2-4)^2+(3-5)^2+(4-6)^2+(5-7)^2)/4=4。

无论是绝对误差还是均方误差，它们都能用来量化模型的预测效果，因此它们也都能反应真实值和预测值之间的匹配程度。当误差越小时，预测结果和真实标记就越接近。当误差最小时，预测结果最贴近真实标记，此时所得到的就是模型最符合训练集数据规律的最优参数。不过它们之间也各有特点，比如绝对误差计算的是误差的绝对值，对异常值不那么敏感，而均方误差计算的是误差的平方值，对于异常值更加敏感，会对误差赋予更严厉的惩罚。所以在使用过程中，我们需要基于实际问题来选择使用哪种代价函数。在这个案例中，我们选择均方误差作为代价函数来计算模型的预测误差，我们设模型参数 w=5w=5、b=10b=10，那么回归方程为 y=5x+10y=5x+10，根据回归方程可以计算出如下 8 个样本的预测值：

image-20241110184525036

然后计算预测值和真实值差异的平方，带入到均方误差公式中，最终求出模型的预测误差是 268.75268.75。

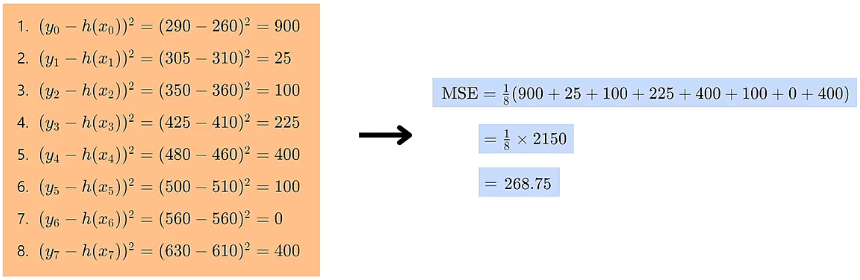
image-20241110192424821

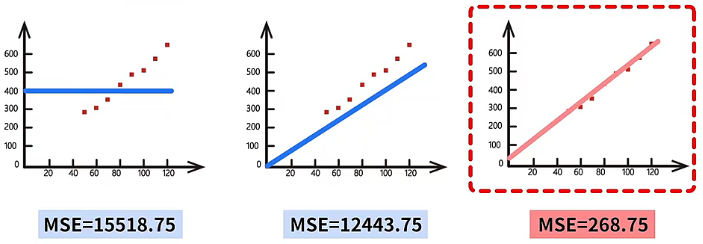
不同的模型参数 ww 和 bb 会计算出不同的均方误差，均方误差越小，模型参数 ww 和 bb 就越合适。例如，下面三条直线中第三条直线的均方误差最小，因此第三条直线就最合适。

image-20241110232400126

求解最优参数 ​

当代价函数计算出来的平均损失达到最小时，模型预测值最贴近训练真实值。上面我们设定的模型参数为 w=5w=5、b=10b=10，通过均方误差计算模型的平均损失为 268.75268.75，这个平均损失达到最小值了吗？显然不能确定。因此，下面我们将通过数学计算方法和梯度下降算法来求得模型的最优参数。

数学计算方法 ​

首先，我们对均方误差公式进行变换，过程如下：

\begin{aligned} MSE&=\frac{1}{m}\sum_{i=1}^{m}(y_i-\widehat y_i)^2\\ &=\frac{1}{m}\sum_{i=1}^{m}((wx_i+b)-\widehat y_i)^2\\ \end{aligned}

梯度下降算法 ​

，损失函数就会用这些误差计算出一个损失值，目的就是寻找最合适的参数 ww 和 bb 让损失值最小，这样就能让。

需要重点说明的是，绝对误差和均方误差各有特点，具体如下：

  • 在绝对误差中，不管预测值和真实值的差距大小，其梯度永远是一个常数，稳定性好。但也有两个问题，其一就是即使预测值和真实值差距特别的大，给出的梯度也不会很大，下降周期慢；其二就是梯度在零点处不可导，在 1 到 -1 之间有一个剧烈的变化，不够平滑，优化到末期的时候，可能会不那么稳定，从而导致跳过极小值。
  • 在均方误差中，梯度大小和预测值和真实值的差距大小相关。当预测值和真实值的差距比较大时，给出的梯度也会比较大，下降周期快。当预测值靠近真实值时，给出的梯度也会逐渐变小。但也有一个问题就是，当预测值与目标值相差很大时，梯度容易爆炸。

在实际使用过程中，我们可以结合以上两种损失函数的特点，当预测值和真实值差距比较大的时候，使用 L1 loss 作为损失函数，当预测值和真实值差距比较小的时候，使用 L2 loss 作为损失函数。

我们就需要通过梯度下降算法精确的找出最优的直线方程参数 ww 和 bb

，这就要基于。

使用梯度下降算法，基于训练数据集，基于面积预测价格。

，未来会使用这个方程，根据自变量的值对因变量进行预测。

线性回归是监督的机器学习模型，在监督学习中需要一个数据集来训练模型，因此数据集也被称为训练集，

寻找直线方程参数的过程是建模过程，也被称为模型的训练过程。在训练时，会将训练数据输入到学习算法中，通过学习算法得到拟合模型。如果学习算法对应一元线性回归，那么拟合得到的模型就是平面上的一条直线，在模型中就会保存直线的方程参数 ww 和 bb 。未来我们会将预测数据输入到这条直线中，来生成预测结果。例如训练出面积和价格的直线方程为

使用模型预测 ​

当我们找到描述面积和价格之间的最佳拟合直线后，使用这条直线根据面积计算价格就是线性回归模型的预测和使用过程。例如，原数据中没有出现 55 平的房子，此时我们在直线上找到横坐标是 55 的点向纵坐标投影，就得到了 55 平米房子的价格是 295 万。

image-20241028224649131

多元线性回归 ​

如果回归分析中，包含了两个或两个以上的自变量，并且因变量和自变量之间的关系是线性关系，那么这个回归就是多元线性回归。例如，上面描述房屋的面积和价格之间的关系使用的是一元线性回归，但实际上影响房屋价格的因素还有很多，除了面积这一特征，房屋价格还可能依赖于地理位置、交通、楼层等等因素。

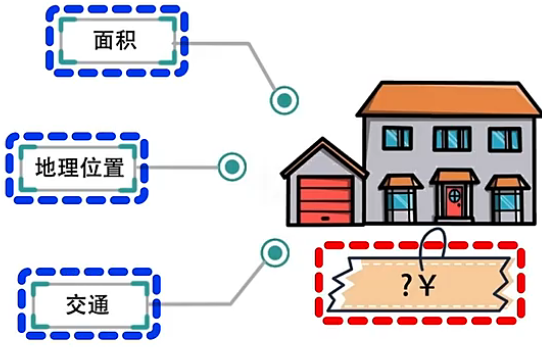
image-20241028233713723

假如我们要描述这些因素对房屋价格的影响，就需要使用多元线性回归，即定义一个包含多个自变量来描述因变量的线性回归，具体如下：定义一个多元函数 f(x1,x2,x3,x4)f(x_1,x_2,x_3,x_4)，其中自变量 x1x_1、x2x_2、x3x_3、x4x_4 分别对应面积、位置、交通和楼层这四个影响房屋价格的因素。

image-20241028234505218

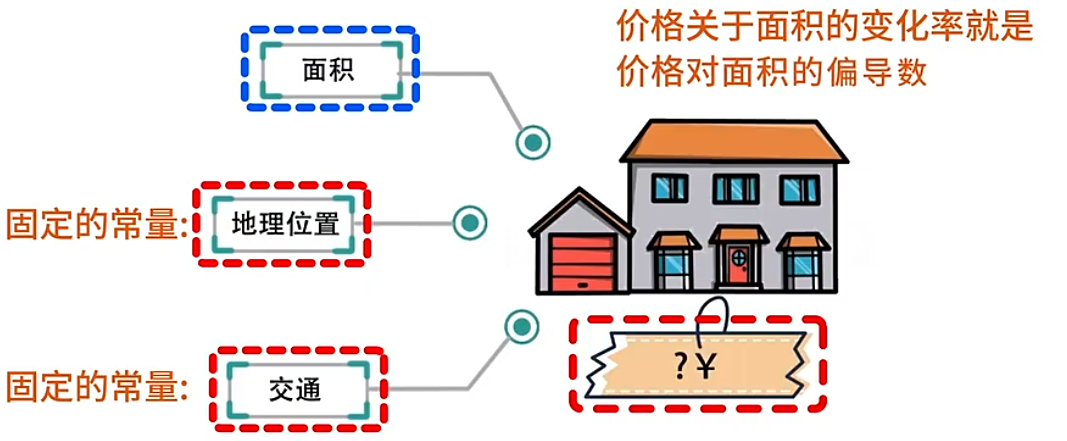
例如，房价和面积、地理位置、交通这三个因素有关，如果将地理位置和交通看做是固定的常量，那么价格关于面积的变化率，就是价格对面积的偏导数

image-20240913231858942

损失函数 ​

。常见的损失函数有如下几种：

  • 交叉熵损失函数(Cross-entropy loss function)
  • 平均绝对误差(Mean Absolute Error，L1_loss)
  • 均方误差(Mean Squared Error，L2_loss)
  • 均方根误差(Root Mean Squared Error)等等......

提醒

这里我们选择 L2 loss 为损失函数 JJ，它就等于每个误差 Δyi\Delta y_i 的平方加和再除以 nn 数据量，因为存在负误差，所以误差 Δyi\Delta y_i 要平方加和，如果正负误差直接相加的话误差会相互抵消。具体内容如下：

J=1n∑i=1n(Δyi2)J=\frac{1}{n}\sum_{i=1}^{n}(\Delta y_i^2)

**现在我们希望这个损失函数 JJ 的值最小，这个值最小就说明此时 y=wx+by=wx+b 模型函数中的参数 ww、参数 bb 的值是最符合房价的价格和面积关系，前面说了它不可能完全符合，因为每一个房价它也可能无法同时满足同一个函数。**那么我们和如何找到最合适的 ww 和 bb 使得损失函数 JJ 的值最小呢？答案就是“梯度下降”。

梯度下降 ​

梯度下降是人工智能最原始、最基础、最核心的一个算法，通过计算训练数据集的梯度，依据损失函数返回的 lossloss 值进行决策，可以帮助我们去处理分类问题，还有回归问题。

算法介绍 ​

现在我们以 ww 值为横坐标，损失函数 JJ 值为纵坐标，在不同的 ww 值下，得到不同的损失函数 JJ 值，我们可能得到如下图像：

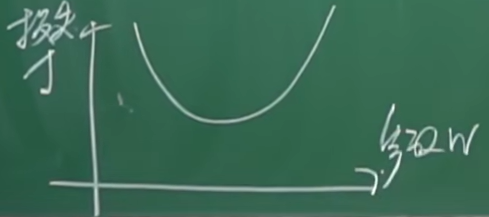
QQ截图20230613145716

现在我们希望找到最优 ww 值使得损失函数 JJ 值的最小，那么我们挑选一个 w0w_0 初始值，但这个 w0w_0 值不一定等于最优 ww 值，于是我们就要使用梯度下降算法了。其中的过程大体是这样：

  • 首先我们要理解一个 ∂\partial 偏导数的概念，损失函数 JJ 值随着 ww 值的变化而变化，就可以使用函数 ∂J∂wi\frac{\partial J}{\partial w_i} 来表示，它反应了当前 wiw_i 值在函数中的倾斜程度，如果斜率越大，说明离最优 ww 值越远，反之就离最优 ww 值越越近；
  • 现在我们求 w0w_0 值在函数中的斜率，也就是求函数 ∂J∂w0\frac{\partial J}{\partial w_0} 的值，当函数值求出来了以后，我们向着 wn+1=wn−η∂J∂wnw_{n+1}=w_n-\eta\frac{\partial J}{\partial w_n} 反梯度的方向进行迭代，通过这种方式，我可以从当前的 w0w_0 值找到更好的 w1w_1 值；
  • 求出 w1w_1 值后，可能还不是最优 ww 值，我们继续去求 w1w_1 值在函数中的倾斜程度，再向着反梯度的方向进行迭代，于是我们又找到了比 w1w_1 值更好的 w2w_2 值；
  • 如果 w2w_2 值已经超过最优 ww 值，那么在下一次迭代时，会反向朝着最优 ww 值进行靠近；
  • 经过这样一次次迭代，到最后当 ∂J∂wi≈0\frac{\partial J}{\partial w_i}\approx{0} 时，也就是 wn+1≈wn{w_{n+1}}\approx{w_{n}} 时，我们就不需要进行迭代了，此时就找到了最优 ww 值。
  • 简单讲，梯度下降就是通过不断沿着梯度的反方向更新模型参数进行求解。

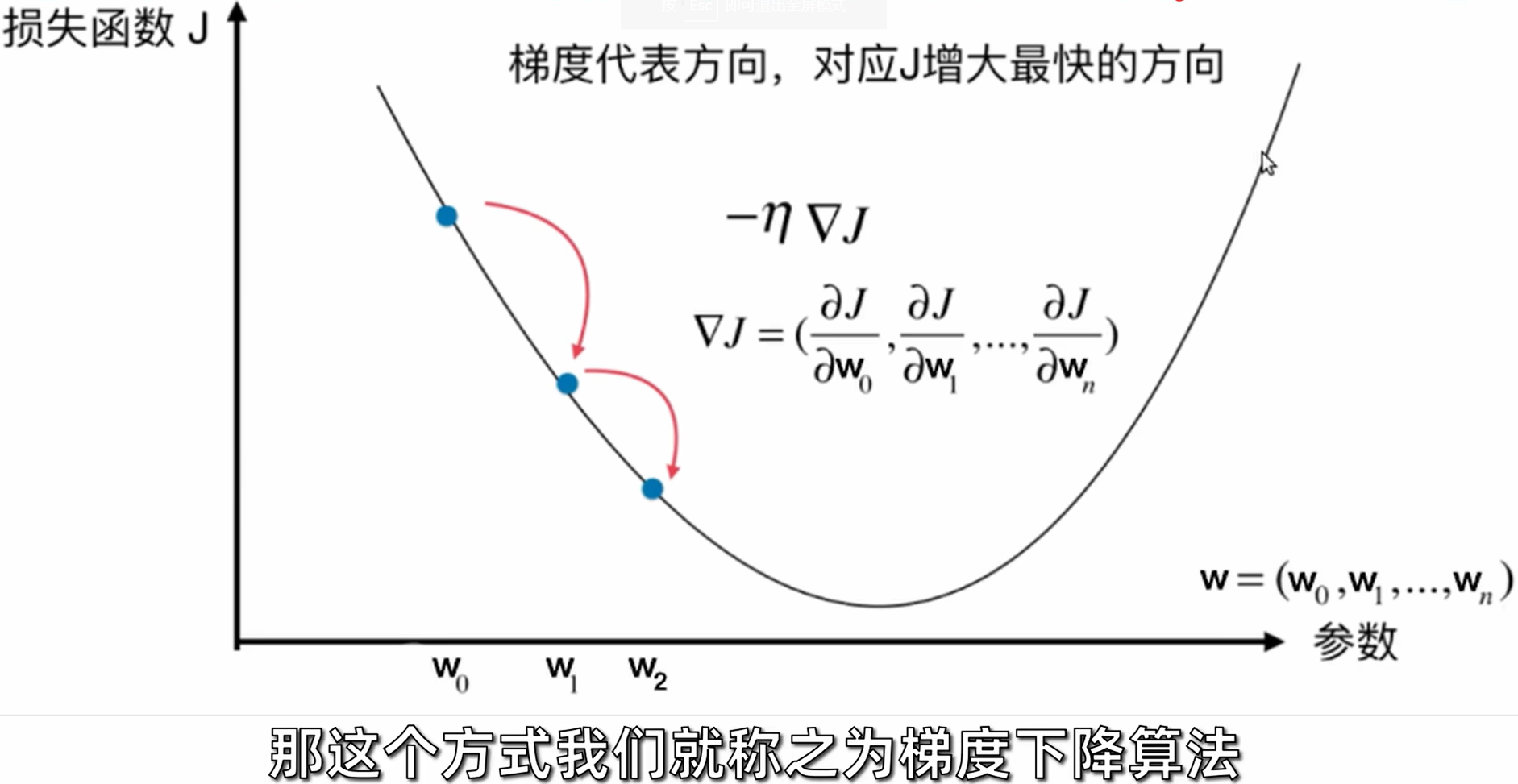
QQ截图20230613153820

选择学习率 ​

现在我们知道了梯度的反方向就是优化的方向，还有一个重要的参数就是“学习率”，也就是梯度下降的步长，对应到迭代公式中就是 η\eta 参数。学习率的选择即不能太小，也不能太大，学习率太小算法需要经过大量迭代才能收敛，也就是训练的慢，学习率太大就是不断地在最优值中左右徘徊，若比之前的起点还要高，这会导致算法发散，值越来越大。下面的例子说明了使用不同的学习率对寻找最优值的影响：

警告

这里我们只考虑了 ww 值，没有考虑 bb 值，我们在进行梯度下降算法的时候，实际上是 ww 值和 bb 值同时进行优化的，相当于我们是在一个三维的空间中寻找一个最低点。

梯度计算 ​

在 Tensor 数据结构中有一个 requires_grad 属性，表示张量是否需要在计算过程中保留对应的梯度信息，默认为 False 表示不保留。如果设置为 True，那么 PyTorch 的自动求导机制会对该张量以及由这个张量计算出来的其他张量进行求导计算，当完成计算后通过调用 .backward() 来自动计算所有的梯度，最后将梯度保存到 .grad 属性。

python
import torch

x = torch.rand(2, requires_grad=True)  # 注释：生成一行二列的张量，其中的元素是在[0,1)范围内均匀分布的随机浮点数。
print(x)            # 输出：tensor([0.6519, 0.7722], requires_grad=True)
y = x.mean()        # 注释：生成x张量的平均值张量赋值给y。
print(y)            # 输出：tensor(0.7121, grad_fn=<MeanBackward0>)。注释：因为y张量通过x张量生成，而且x张量的requires_grad为True，因此输出的y张量带有与平均操作关联的grad_fn梯度函数。
y.backward()        # 注释：计算梯度值，保存在x张量的grad属性中。
print(x.grad.data)  # 输出：tensor([0.5000, 0.5000])。注释：在计算y的均值时，每个元素对于均值的梯度都是0.5000。
y.backward()
print(x.grad.data)  # 输出：tensor([1., 1.])。注释：梯度会自动累积。
x.grad.zero_()      # 注释：将x的梯度清零。
y.backward()
print(x.grad.data)  # 输出：tensor([0.5000, 0.5000])

[!ATTENTION]

在PyTorch中，默认梯度不清零并且会累加梯度，因此在使用时要注意梯度清零。

常见形式 ​

梯度下降算法有三种常见的形式：批量梯度下降(BGD)、随机梯度下降(SGD)、小批量梯度下降(MBGD)。

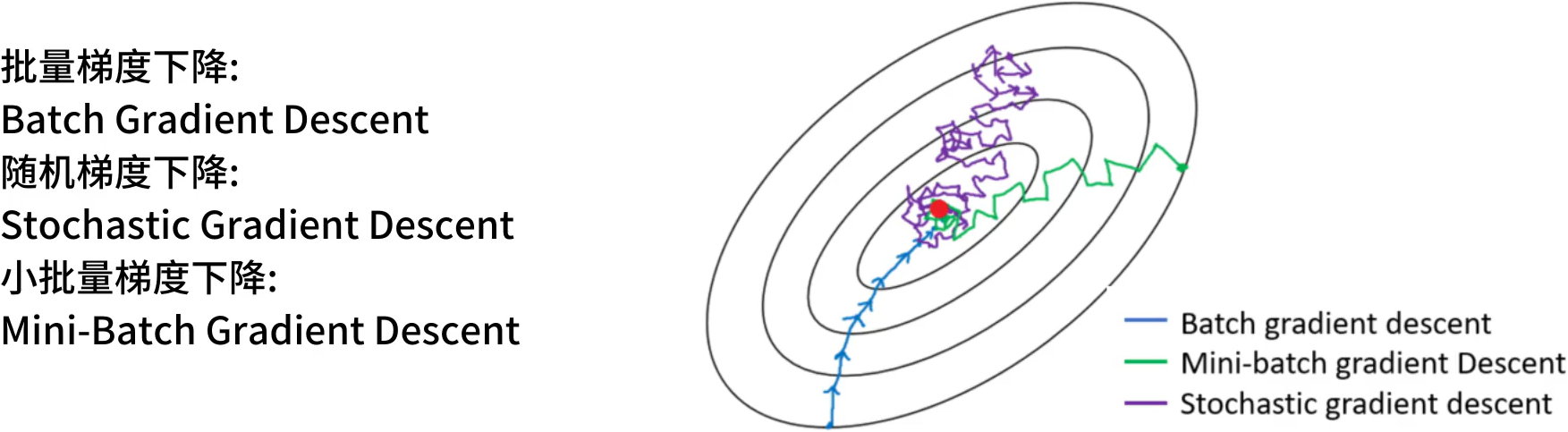
QQ截图20230814143427

批量BGD ​

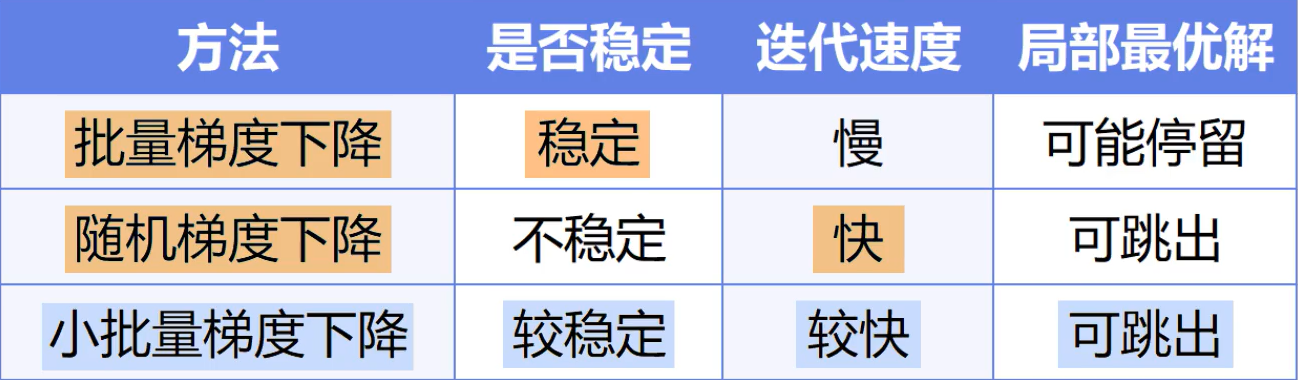
**批量梯度下降(BGD)：每次迭代都会基于所有的训练样本，计算损失函数的梯度。**例如，训练集中有100个样本，迭代50轮，在每一轮迭代中会使用整个训练集这100个样本计算梯度，并对模型更新，所以总共会更新50次梯度，而我们也可以得到一条平滑的收敛曲线。

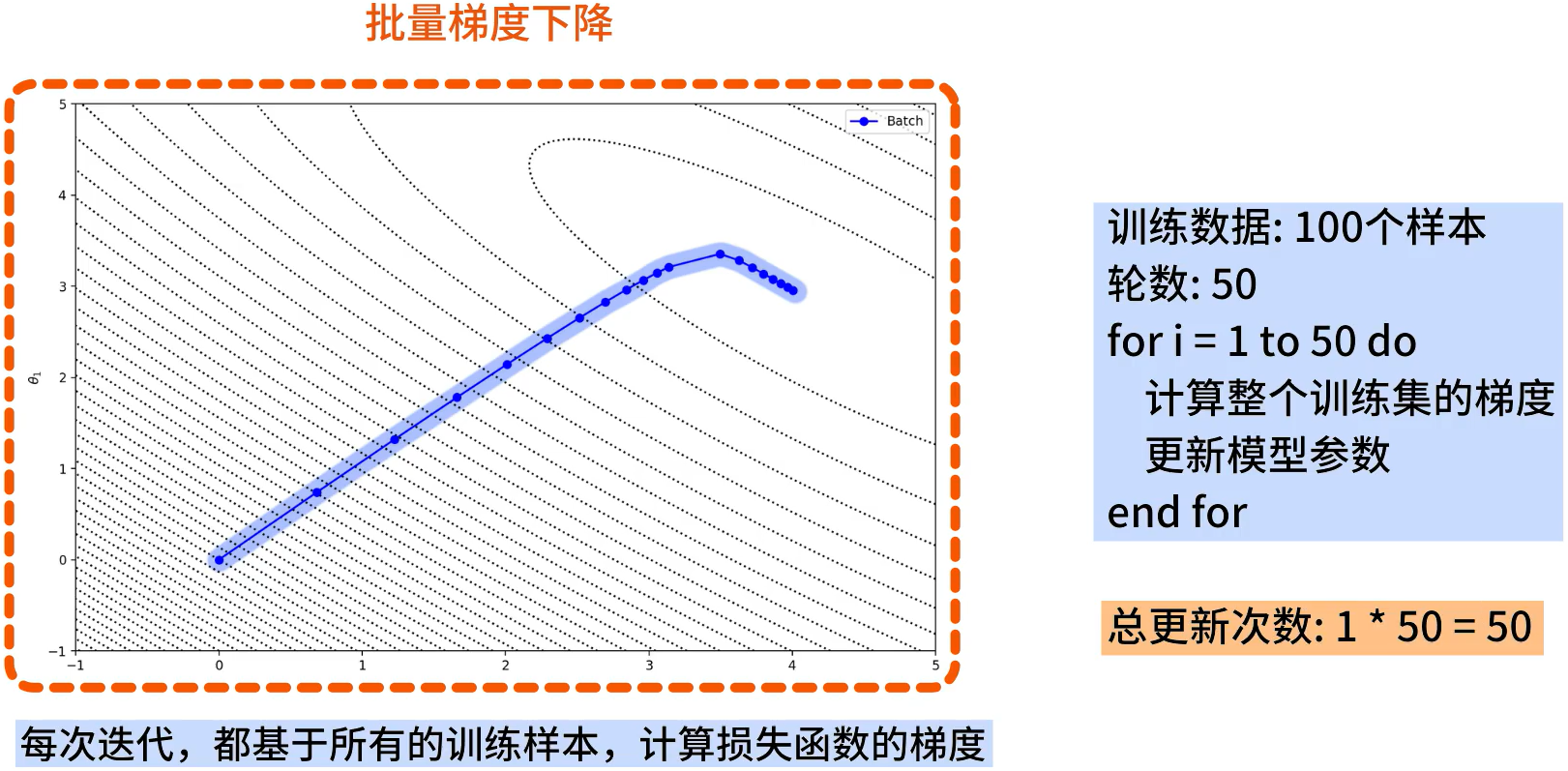
QQ截图20230814150149

批量梯度下降(BGD)的特点如下：每一次梯度的下降过程中都会计算梯度，这意味着要把整个样本给重新算一遍，这样可以得到准确的梯度方向，但在实际生产环境中这个数据量往往是很大的，这么做是一件费时费力事，计算一个深度神经网络模型下降梯度可能需要数分钟至数小时，很影响算法的性能。

QQ截图20230814150718

随机SGD ​

**随机梯度下降(SGD)：会在一轮完整的迭代过程中遍历整个训练集，但是每次更新都只基于一个样本计算梯度。**例如，训练集中有100个样本，迭代50轮，每一轮迭代都会随机不放回的抽取完这100个样本，每次计算某一个样本的梯度，然后更新模型参数，所以总共会更新5000次梯度，而我们会得到一条振荡的收敛曲线。

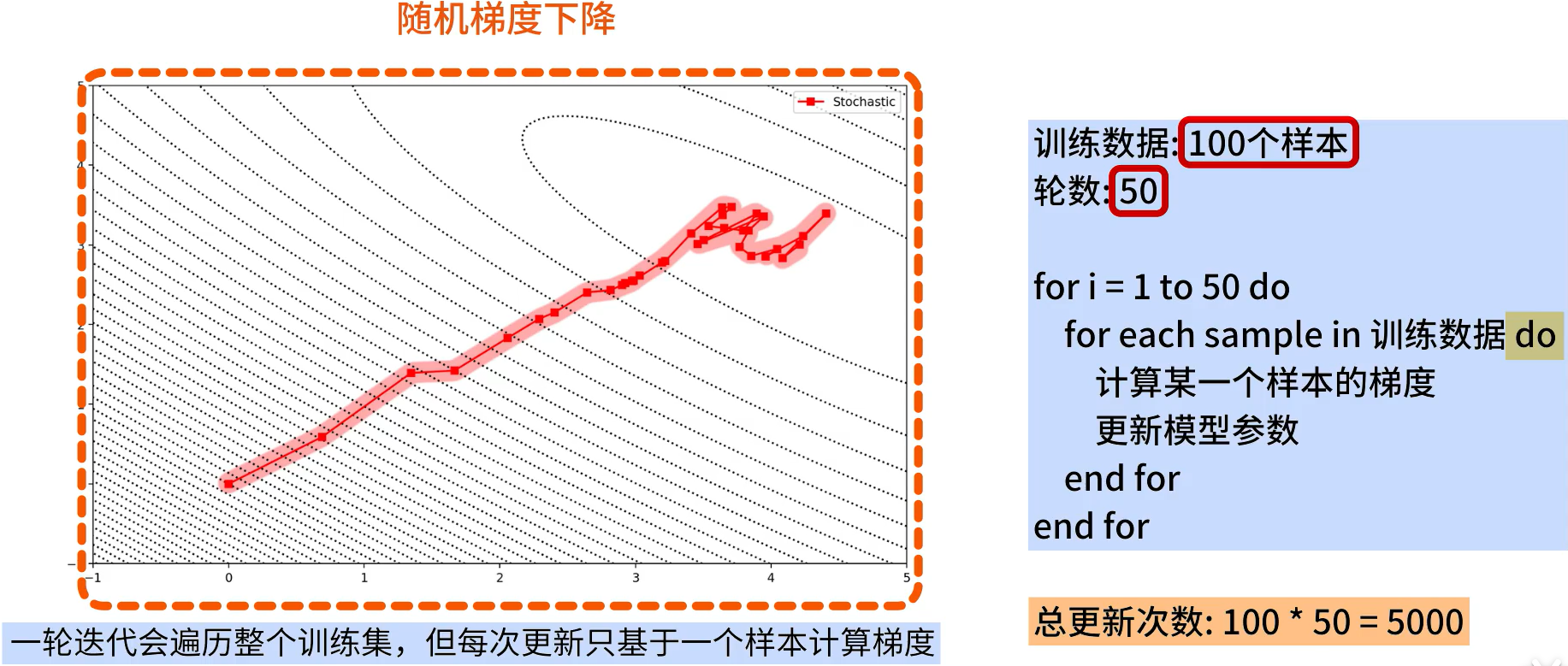
QQ截图20230814151426

随机梯度下降(SGD)的特点如下：因为每次只用一个样本进行训练，所以迭代速度会非常快，但更新的方向会不稳定，这也导致随机梯度下降可能永远都不会真正的收敛，不过也因为这种震荡属性，使得随机梯度下降，可以跳出局部最优解，这在某些情况下是非常有用的。

QQ截图20230814151658

小批量MBGD ​

**小批量梯度下降(MBGD)：每次迭代都会从训练集中随机的选择一组小批量的样本，来计算梯度，更新模型参数。**例如，训练集中有100个样本，迭代50轮，如果设置小批量的数量是20，在每一轮迭代中都会随机不放回的抽取完这5个小批量，每次计算某一个小批量的梯度，并对模型更新，所以总共会更新250次梯度，而我们也可以得到一条相对平滑的收敛曲线。

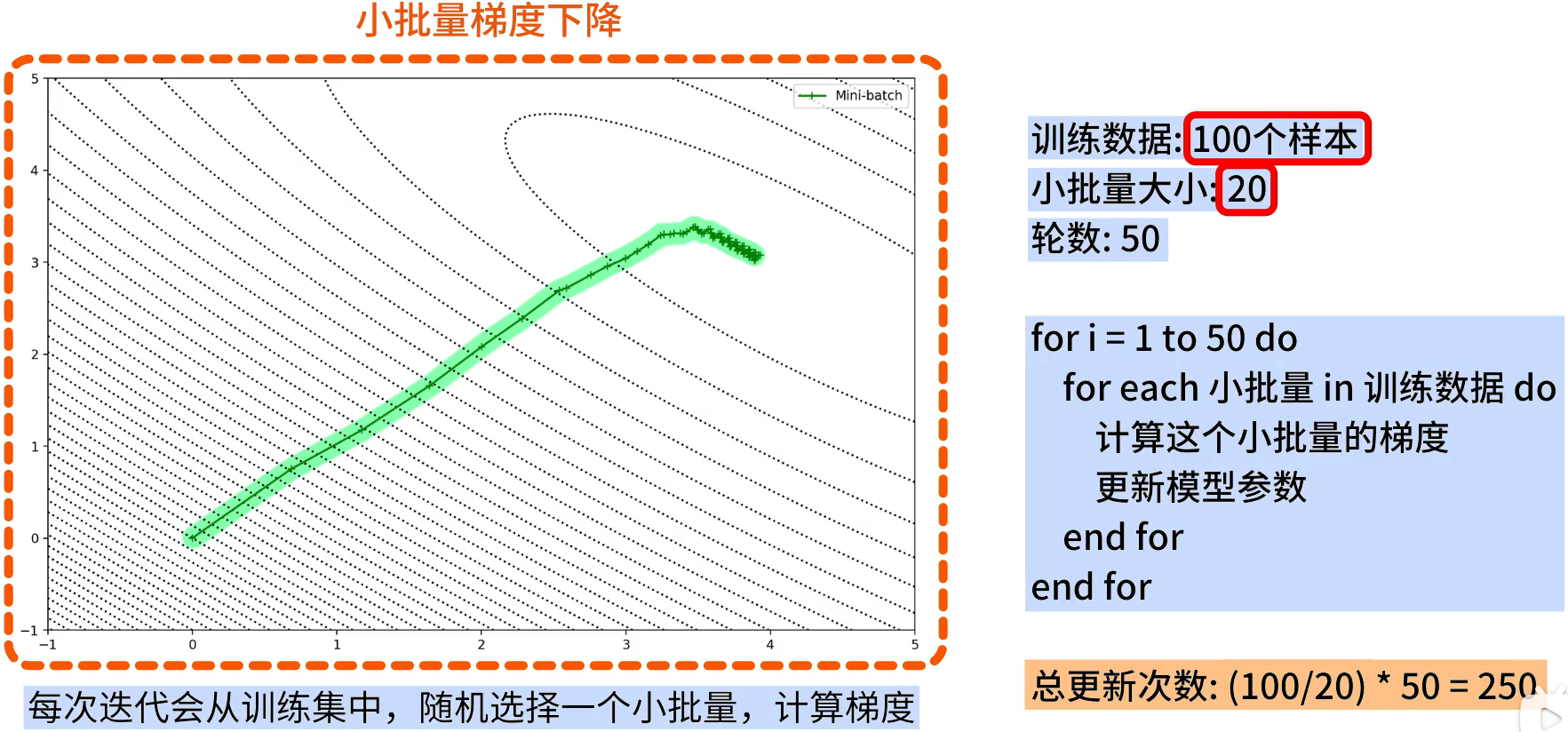
QQ截图20230814153931

小批量梯度下降(MBGD)的特点如下：结合了随机梯度下降的高效性和批量梯度下降的稳定性，它比随机梯度下降有更稳定的收敛，同时又比批量梯度下降计算的更快。另外，由于小批量的随机性，还能使迭代跳出局部最优解，因此小批量梯度下降是深度学习默认的模型训练方式。

QQ截图20230814154110

提醒

若整个数据集的大小不是批量的大小的整数倍，有两种解决办法：一种是舍弃最后不足一个批量大小的数据，另一种是从数据集的开头补足最后的数据至一个批量的大小。

警告

批量大小同学习率一样，不能太小，否则每次计算量太小，不适合并行来最大利用计算资源，当然也不能太大，否则内存消耗增加，浪费计算资源。

拟合线性函数 ​

现在，我们基于上面房价的线性回归问题来说明如何实现拟合线性函数。

随机种子 ​

首先我们要理解一个随机种子的概念，先来看看下面的代码：代码中使用了 Numpy 生成随机数的操作，可以看到两次该代码所生成的随机数都不相同。

python
'''第一次运行'''
import numpy as np

# 生成随机数
random_numbers = np.random.rand(3)
print(random_numbers)  # 输出：[0.32891826 0.02494823 0.86303608]
random_numbers = np.random.rand(3)
print(random_numbers)  # 输出：[0.44638722 0.8519038  0.23821016]
python
'''第二次运行'''
import numpy as np

# 生成随机数
random_numbers = np.random.rand(3)
print(random_numbers)  # 输出：[0.6988882  0.27195866 0.17775636]
random_numbers = np.random.rand(3)
print(random_numbers)  # 输出：[0.10365368 0.3641671  0.28024424]

在机器学习和数据分析中，模型训练、数据切分常常会涉及到数据随机性操作，为了实现结果的可重复性，我们希望在不同的机器上得到相同的随机数，即随机性一致，该怎样操作呢？答案就是设置随机种子。下面的代码中增加了一个种子值为 42 的随机种子，这样不管在哪台机器上运行以及何时运行该程序，所得到的随机数都是一样，可以看到第一次运行中第一次输出的随机数和第二次运行中第一次输出的随机数一样，第一次运行中第二次输出的随机数和第二次运行中第二次输出的随机数也一样，说明设置随机种子会影响整个代码中使用到的 NumPy 随机数生成器的状态。

python
'''第一次运行'''
import numpy as np

# 设置一个种子值为42的随机种子
np.random.seed(42)
# 生成随机数
random_numbers = np.random.rand(3)
print(random_numbers)  # 输出：[0.37454012 0.95071431 0.73199394]
random_numbers = np.random.rand(3)
print(random_numbers)  # 输出：[0.59865848 0.15601864 0.15599452]
python
'''第二次运行'''
import numpy as np

# 设置一个种子值为42的随机种子
np.random.seed(42)
# 生成随机数
random_numbers = np.random.rand(3)
print(random_numbers)  # 输出：[0.37454012 0.95071431 0.73199394]
random_numbers = np.random.rand(3)
print(random_numbers)  # 输出：[0.59865848 0.15601864 0.15599452]

**任何整数均可作为随机数生成器的种子值，不同的种子值将导致不同的初始状态，从而产生不同的随机数序列。在实际应用中，种子值的范围并没有具体的限制，通常可以是任何整数。常见的选择是正整数，通常是较大的数，以确保更好的随机性。**使用小于或等于 32 位整数范围的种子可能会导致周期较短的随机数序列。具体如下代码：可以看到，选择不同的种子值，最后得到了不同的随机数序列。

python
'''第一次运行'''
import numpy as np

# 设置一个种子值为42的随机种子
np.random.seed(42)
# 生成随机数
random_numbers = np.random.rand(3)
print(random_numbers)  # 输出：[0.37454012 0.95071431 0.73199394]
random_numbers = np.random.rand(3)
print(random_numbers)  # 输出：[0.59865848 0.15601864 0.15599452]
python
'''第二次运行'''
import numpy as np

# 设置一个种子值为43的随机种子
np.random.seed(43)
# 生成随机数
random_numbers = np.random.rand(3)
print(random_numbers)  # 输出：[0.11505457 0.60906654 0.13339096]
random_numbers = np.random.rand(3)
print(random_numbers)  # 输出：[0.24058962 0.32713906 0.85913749]

训练数据 ​

现在开始生成训练数据，假定房价数据遵循 房价=3*面积+4+噪音 规律，生成数据的代码如下：

python
import matplotlib.pyplot as plt
import numpy as np

# 设置一个固定的随机种子，确保每次运行都得到相同的数据，方便调试。
np.random.seed(42)
# 随机生成100个横坐标x，范围在0到2之间
x = 2 * np.random.rand(100, 1)
# 数据基本分布在y=3x+4的附近，生成带有噪音的纵坐标
y = 3 * x + 4 + np.random.randn(100, 1) * 0.5
# 生成在画板上
plt.scatter(x, y, marker='x', color='red')
plt.show()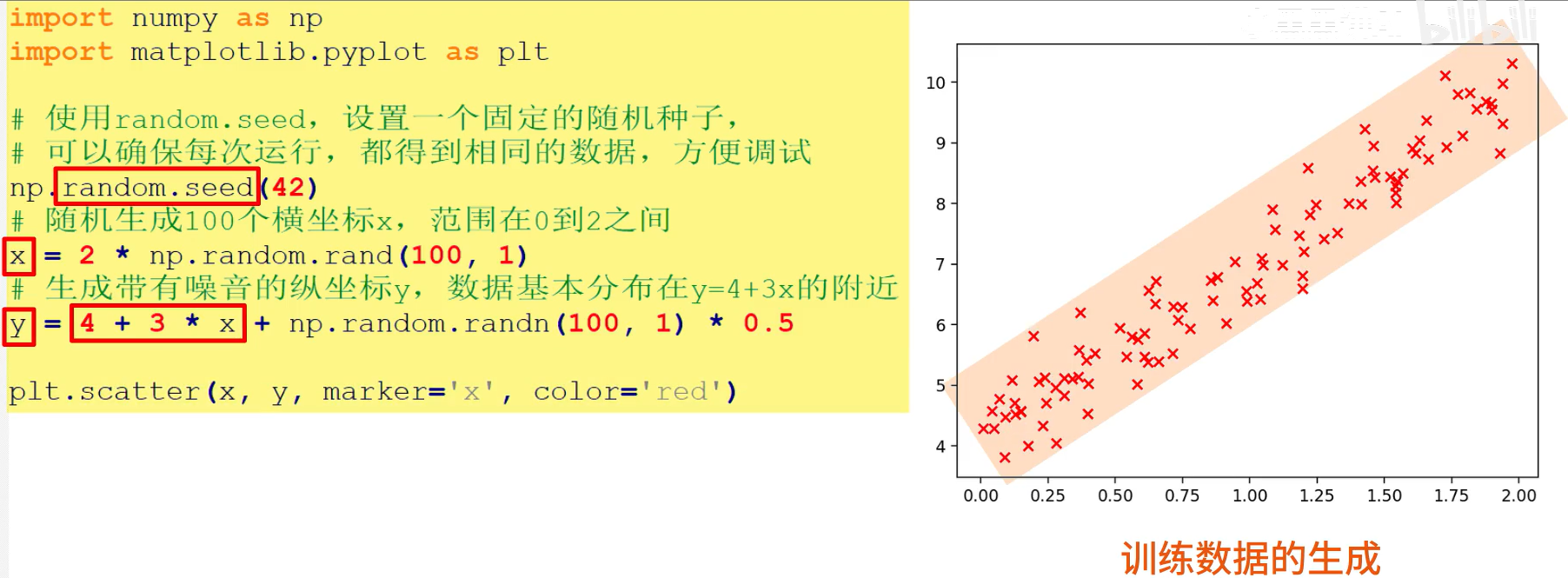

QQ截图20230814160431

建议

若出现 AttributeError: module 'numpy' has no attribute 'ndarray' 则说明numpy与pandas版本不匹配，卸载当前的numpy与pandas，重新安装一下 pip install numpy==1.21.5 和 pip install pandas==1.4.3 即可。

随机小批量 ​

接着我们将 numpy 的数据转换为 PyTorch 可用的 Tensor 数据结构，打包成一个数据集，将数据集里的数据随机打乱，再分为大小为 16 的 7 个小批量：

python
import torch
from torch.utils.data import DataLoader, TensorDataset

# 将训练数据x和y转为张量
x = torch.from_numpy(x).float()
y = torch.from_numpy(y).float()
# 使用TensorDataset将x和y组成训练集
dataset = TensorDataset(x, y)
# 使用DataLoader构造随机的小批量数据，每个一个小批量的数据规模是16，随机打乱数据的顺序
dataloader = DataLoader(dataset=dataset, batch_size=16, shuffle=True)

QQ截图20230814160646

实现梯度下降 ​

以这里的线性回归为例，权重 w 和偏置 b 为需要训练的对象，为了得到最合适的参数值，需要根据梯度回传思路进行训练，即只要某一个输入需要相关梯度值，则输出也需要保存相关梯度信息，这样就保证了这个输入的梯度回传，因此就需要将 requires_grad 属性设置 True。代码如下：

python
# 待迭代的参数为w和b
w = torch.randn(1, requires_grad=True)
b = torch.randn(1, requires_grad=True)
# 进入模型的循环迭代
for epoch in range(1, 51):  # 代表了整个训练数据集的迭代轮数
    # 在一个迭代轮次中，以小批量的方式，使用dataloader对数据进行遍历
    # batch_idx表示当前遍历的批次
    # data和label表示这个批次的训练数据和标记
    for batch_idx, (data, label) in enumerate(dataloader):
        h = x * w + b  # 计算当前直线的预测值，保存到h
        # 计算预测值h和真实值y之间的均方误差，保存到loss中
        loss = torch.mean((h - y) ** 2)
        loss.backward()  # 计算代价loss关于参数w和b的偏导数
        # 进行梯度下降，沿着梯度的反方向，更新w和b的值
        w.data -= 0.01 * w.grad.data
        b.data -= 0.01 * b.grad.data
        # 清空张量w和b中的梯度信息，为下一次迭代做准备
        w.grad.zero_()
        b.grad.zero_()
        # 每次迭代，都打印当前迭代的论述epoch
        # 数据的批次batch_idx和loss损失值
        print(f"epoch({epoch}) batch({batch_idx}) loss={loss.item():.3f}")

image-20231221155555168

建议

在使用小批量梯度下降法训练神经网络时，我们会将训练数据分成多个小批量，每次只使用一个小批量的数据进行反向传播来计算梯度并更新模型参数。如果不清零梯度，每次计算的梯度都会累加在一起，这叫做梯度累加，会导致模型的更新不准确。另外，在使用神经网络时，全连接层卷积层等结构的参数都是默认需要梯度的。

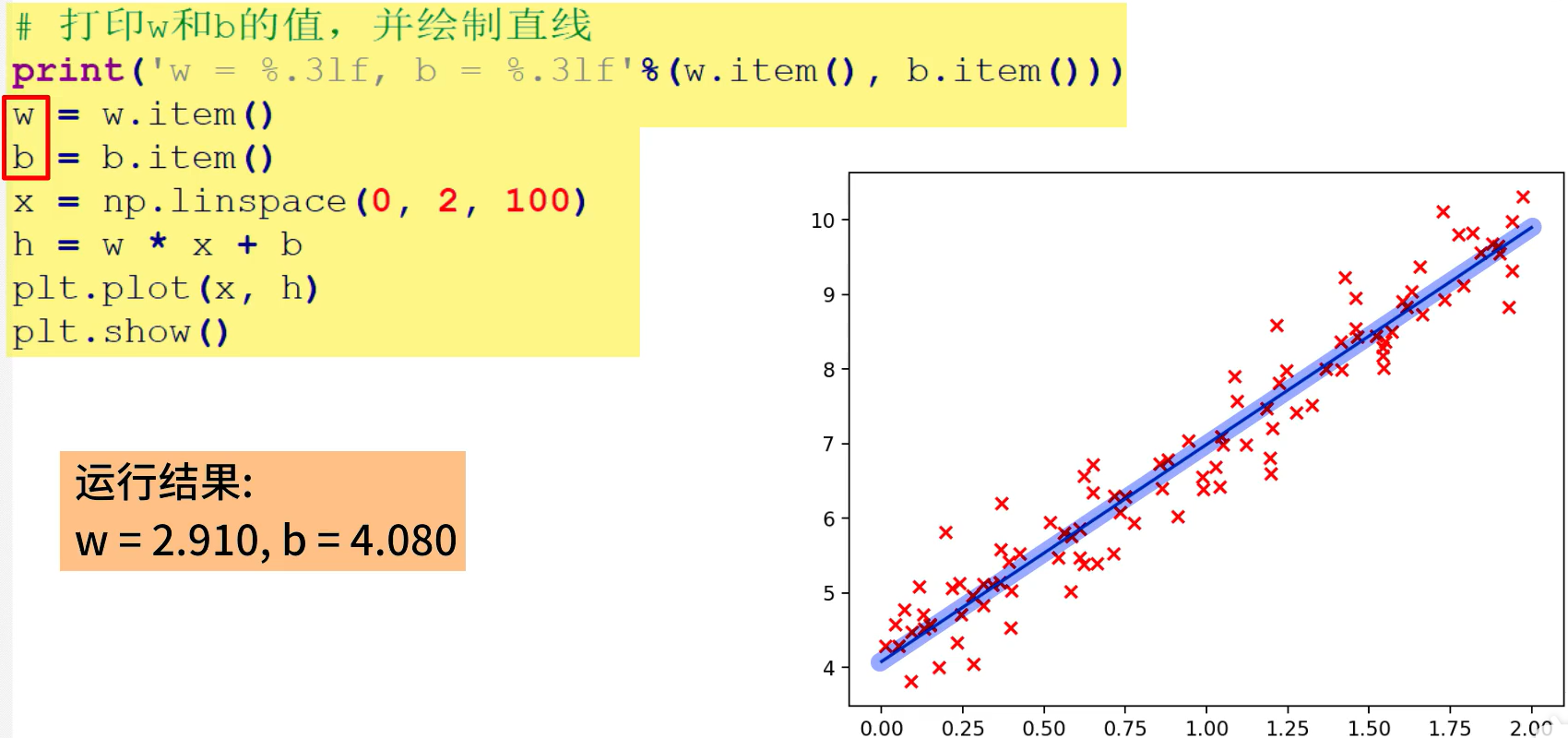
结果可视化 ​

python
# 打印w和b的值，并绘制直线
print(f'w={w.item()}, b={b.item()}')
w = w.item()
b = b.item()
x = np.linspace(0, 2, 100)
h = w * x + b
plt.plot(x, h)
plt.show()

QQ截图20230814161124