剑眉星目

深浅模式

复杂度分析 ​

更新: 2025/2/24 字数: 0 字 时长: 0 分钟

前面我们介绍了算法（Algorithm），简单讲就是解决问题的方法。对于同一个问题，使用不同的算法，最终得到的结果一样，但在过程中消耗的资源和时间却会有很大的区别。在算法设计中，我们先后追求以下两个层面的目标：

  1. 找到问题解法：算法需要在规定的输入范围内可靠地求得问题的正确解。
  2. 寻求最优解法：同一个问题可能存在多种解法，我们希望找到尽可能高效的算法。

简而言之，我们的目标是设计“既快又省”的数据结构与算法。因此有效地评估算法效率至关重要，因为只有这样，我们才能将各种算法进行对比，进而指导算法设计与优化过程。由于算法在实际测试中会受硬件配置、系统平台、编译器或解释器的优化、数据体量大小的影响进而展现出不同的效率，因此我们需要一个估算方法来评估算法的效率，该估算方法被称为“渐近复杂度分析（asymptotic complexity analysis）”，简称“复杂度分析”。它描述了随着输入数据大小的增加，算法执行所需时间和空间的增长趋势，即算法运行所需的时间和空间资源与输入数据大小之间的关系。因此评估一个算法效率，主要包括以下两个维度：

  • 时间复杂度：指算法运行过程中所消耗的时间长短。
  • 空间复杂度：指算法运行过程中所占用的内存大小。

建议

复杂度分析独立测试环境，分析结果适用于所有运行平台，并且可以体现不同数据量下的算法效率，尤其是在大数据量下的算法性能。可以说，复杂度分析为我们提供了一把评估算法效率的“标尺”，使我们可以衡量执行某个算法所需的时间和空间资源，对比不同算法之间的效率。

时间复杂度 ​

时间复杂度分析统计的不是算法运行时间，而是算法运行时间随着数据量变大时的增长趋势。这个概念比较抽象，我们通过一个例子来加以理解。假设输入数据大小为 nn ，给定三个算法 A、B 和 C ：

python
# 算法 A 的时间复杂度：常数阶
def algorithm_A(n: int):
    print(0)

# 算法 B 的时间复杂度：线性阶
def algorithm_B(n: int):
    for _ in range(n):
        print(0)

# 算法 C 的时间复杂度：常数阶
def algorithm_C(n: int):
    for _ in range(1000000):
        print(0)

下图展示了以上三个算法函数的时间复杂度。

  • 算法 A 只有 1 个打印操作，算法运行时间不随着 nn 增大而增长。我们称此算法的时间复杂度为“常数阶”。
  • 算法 B 中的打印操作需要循环 nn 次，算法运行时间随着 nn 增大呈线性增长。此算法的时间复杂度被称为“线性阶”。
  • 算法 C 中的打印操作需要循环 10000001000000 次，虽然运行时间很长，但它与输入数据大小 nn 无关。因此 C 的时间复杂度和 A 相同，仍为“常数阶”。

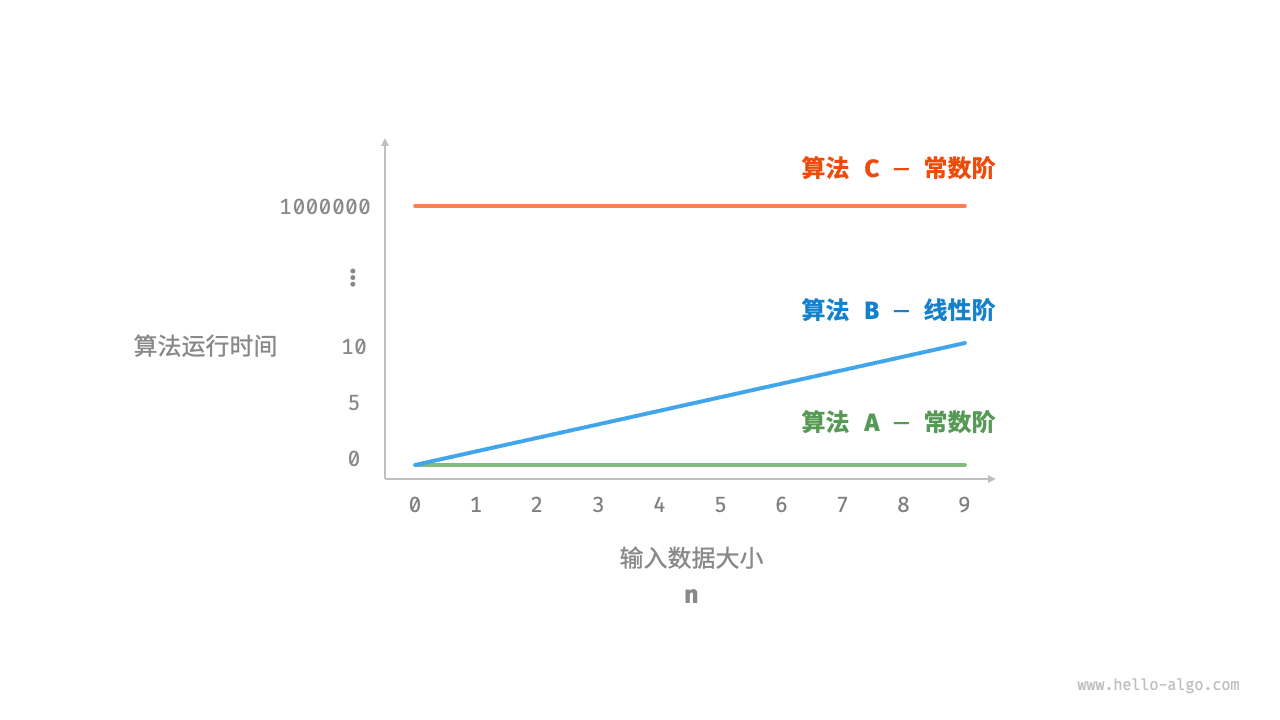
算法 A、B 和 C 的时间增长趋势

相较于直接统计算法的运行时间，时间复杂度分析有哪些特点呢？

  • 时间复杂度能够有效评估算法效率。例如，算法 B 的运行时间呈线性增长，在 n>1n>1 时比算法 A 更慢，在 n>1000000n>1000000 时比算法 C 更慢。事实上，只要输入数据大小 nn 足够大，复杂度为“常数阶”的算法一定优于“线性阶”的算法，这正是时间增长趋势的含义。
  • 时间复杂度的推算方法更简便。显然，运行平台和计算操作类型都与算法运行时间的增长趋势无关。因此在时间复杂度分析中，我们可以简单地将所有计算操作的执行时间视为相同的“单位时间”，从而将“计算操作运行时间统计”简化为“计算操作数量统计”，这样一来估算难度就大大降低了。
  • 时间复杂度也存在一定的局限性。例如，尽管算法 A 和 C 的时间复杂度相同，但实际运行时间差别很大。同样，尽管算法 B 的时间复杂度比 C 高，但在输入数据大小 nn 较小时，算法 B 明显优于算法 C 。在这些情况下，我们很难仅凭时间复杂度判断算法效率的高低。当然，尽管存在上述问题，复杂度分析仍然是评判算法效率最有效且常用的方法。

推算方法 ​

统计操作数量 ​

给定一个输入大小为 nn 的函数：

python
def algorithm(n: int):
    a = 1      # +1
    a = a + 1  # +1
    a = a * 2  # +1
    # 循环 n 次
    for i in range(n):  # +1
        print(0)        # +1

设算法的操作数量是一个关于输入数据大小 nn 的函数，记为 T(n)T(n) ，则以上函数的操作数量为：

T(n)=3+2nT(n)=3+2n

T(n)T(n) 是一次函数，说明其运行时间的增长趋势是线性的，因此它的时间复杂度是线性阶。

判断渐进上界 ​

我们将上面一次函数 T(n)T(n) 线性阶的时间复杂度记为 O(n)O(n) ，这个数学符号称为大 OO 记号（big-OO notation），表示函数 T(n)T(n) 的渐近上界（asymptotic upper bound）。稍微有点数学基础的人就能看出来，在 nn 趋于无穷大时，最高阶的项将发挥主导作用，其他项的影响都可以忽略，因此时间复杂度由 T(n)T(n) 中最高阶的项来决定。下表展示了一些例子，其中一些夸张的值是为了强调“系数无法撼动阶数”这一结论。当 nn 趋于无穷大时，这些常数变得无足轻重。

image-20240516153503209

建议

时间复杂度分析本质上是计算“操作数量 T(n)T(n)”的渐近上界，它具有明确的数学定义。

常见类型 ​

设输入数据大小为 nn ，常见的时间复杂度类型如下图所示（按照从低到高的顺序排列）。

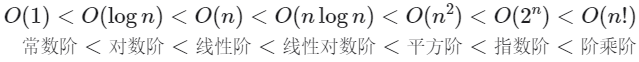
image-20240516153651159

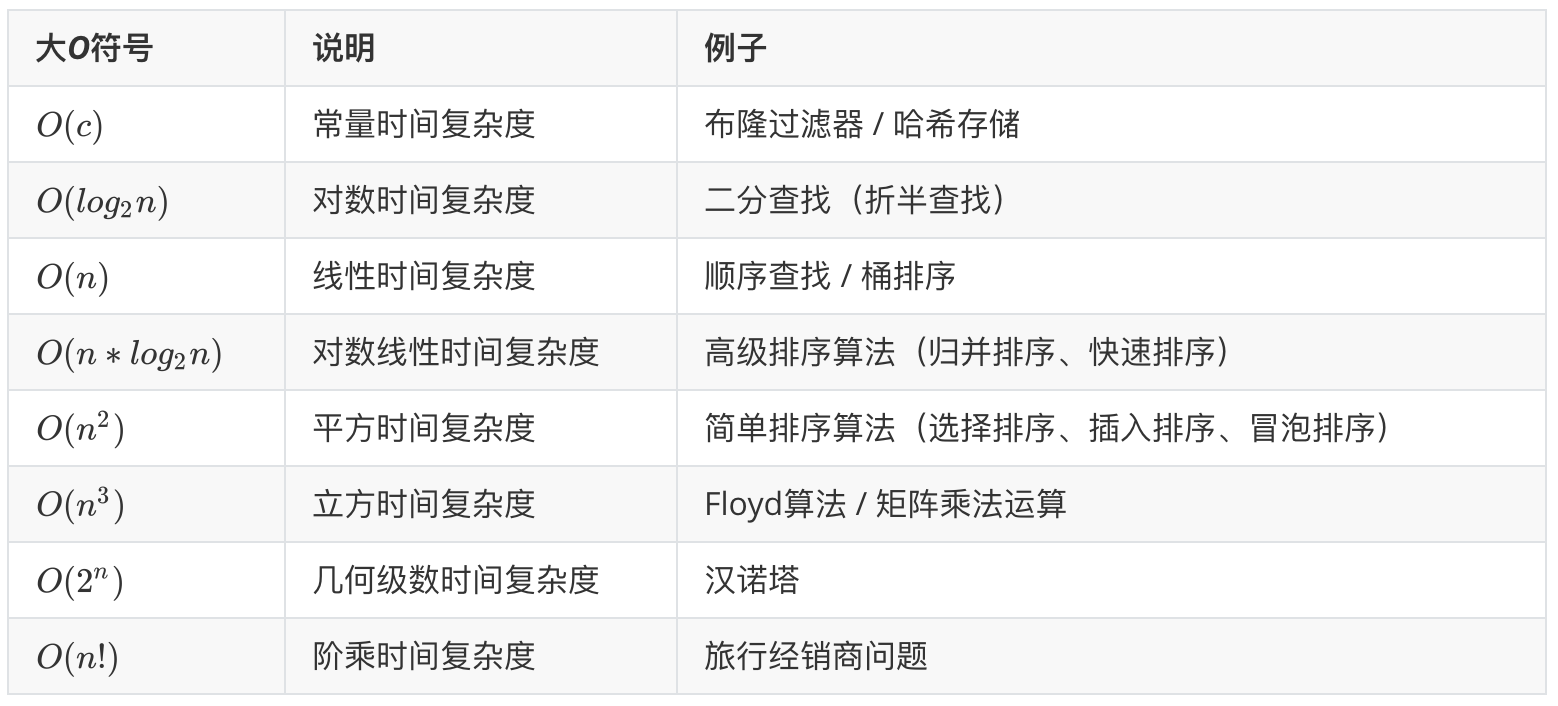
156941

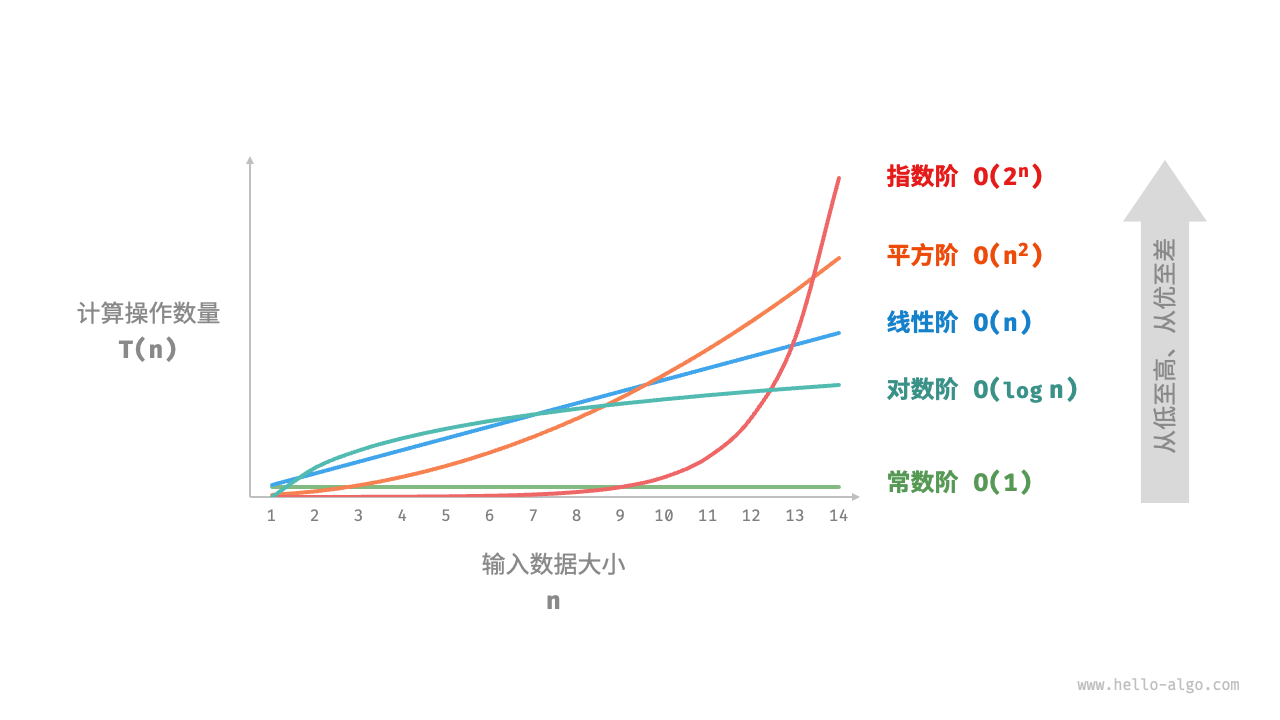
常见的时间复杂度类型

建议

随着数据体量的不断增大，时间复杂度越高的算法，其计算操作数量的上升趋势就会显著。

常数阶 ​

常数阶的操作数量与输入数据大小 nn 无关，即不随着 nn 的变化而变化。在以下函数中，尽管操作数量 size 可能很大，但由于其与输入数据大小 nn 无关，因此时间复杂度仍为 O(1)O(1) ：

python
def constant(n: int) -> int:
    """常数阶"""
    count = 0
    size = 100000
    for _ in range(size):
        count += 1
    return count

建议

在我们设计算法的时候，最理想的时间复杂度是“常量时间复杂度”，因为“常量时间复杂度”算法的运行时间不会随着问题规模的增大而增加，最经典的例子就是哈希表，在 Python 中的 dict 字典、set 集合都有使用。

线性阶 ​

线性阶的操作数量相对于输入数据大小 nn 以线性级别增长。线性阶通常出现在单层循环中：

python
def linear(n: int) -> int:
    """线性阶"""
    count = 0
    for _ in range(n):
        count += 1
    return count

遍历数组和遍历链表等操作的时间复杂度均为 O(n)O(n) ，其中 nn 为数组或链表的长度：

python
def array_traversal(nums: list[int]) -> int:
    """线性阶（遍历数组）"""
    count = 0
    # 循环次数与数组长度成正比
    for num in nums:
        count += 1
    return count

建议

值得注意的是，输入数据大小 nn 需根据输入数据的类型来具体确定。比如在第一个示例中，变量 nn 为输入数据大小；在第二个示例中，数组长度 nn 为数据大小。

平方阶 ​

平方阶的操作数量相对于输入数据大小 𝑛 以平方级别增长。平方阶通常出现在嵌套循环中，外层循环和内层循环的时间复杂度都为 O(n)O(n) ，因此总体的时间复杂度为 O(n2)O(n^2) ：

python
def quadratic(n: int) -> int:
    """平方阶"""
    count = 0
    # 循环次数与数据大小 n 成平方关系
    for i in range(n):
        for j in range(n):
            count += 1
    return count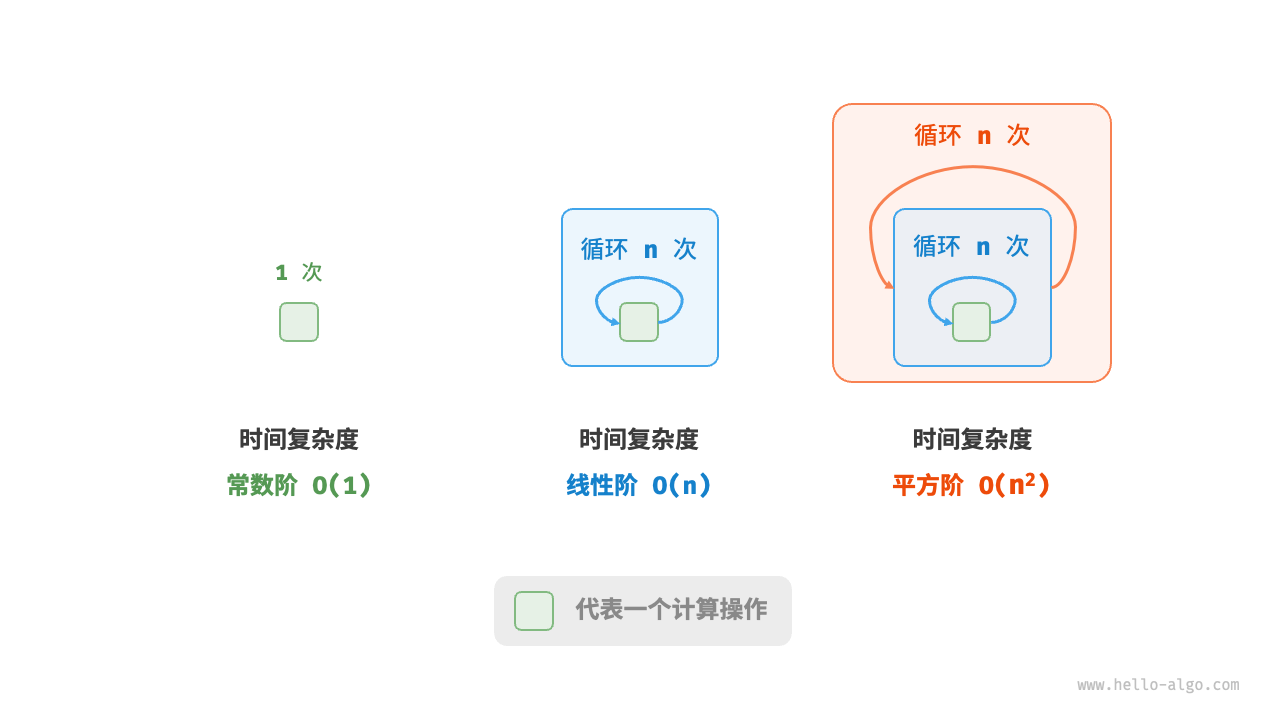

常数阶、线性阶和平方阶的时间复杂度

指数阶 ​

生物学的“细胞分裂”是指数阶增长的典型例子：初始状态为 11 个细胞，分裂一轮后变为 22 个，分裂两轮后变为 44 个，以此类推，分裂 nn 轮后有 2n2^n 个细胞。以下代码模拟了细胞分裂的过程，时间复杂度为 O(2n)O(2^n) ：

python
def exponential(n: int) -> int:
    """指数阶（循环实现）"""
    count = 0
    base = 1
    # 细胞每轮一分为二，形成数列 1, 2, 4, 8, ..., 2^(n-1)
    for _ in range(n):
        for _ in range(base):
            count += 1
        base *= 2
    # count = 1 + 2 + 4 + 8 + .. + 2^(n-1) = 2^n - 1
    return count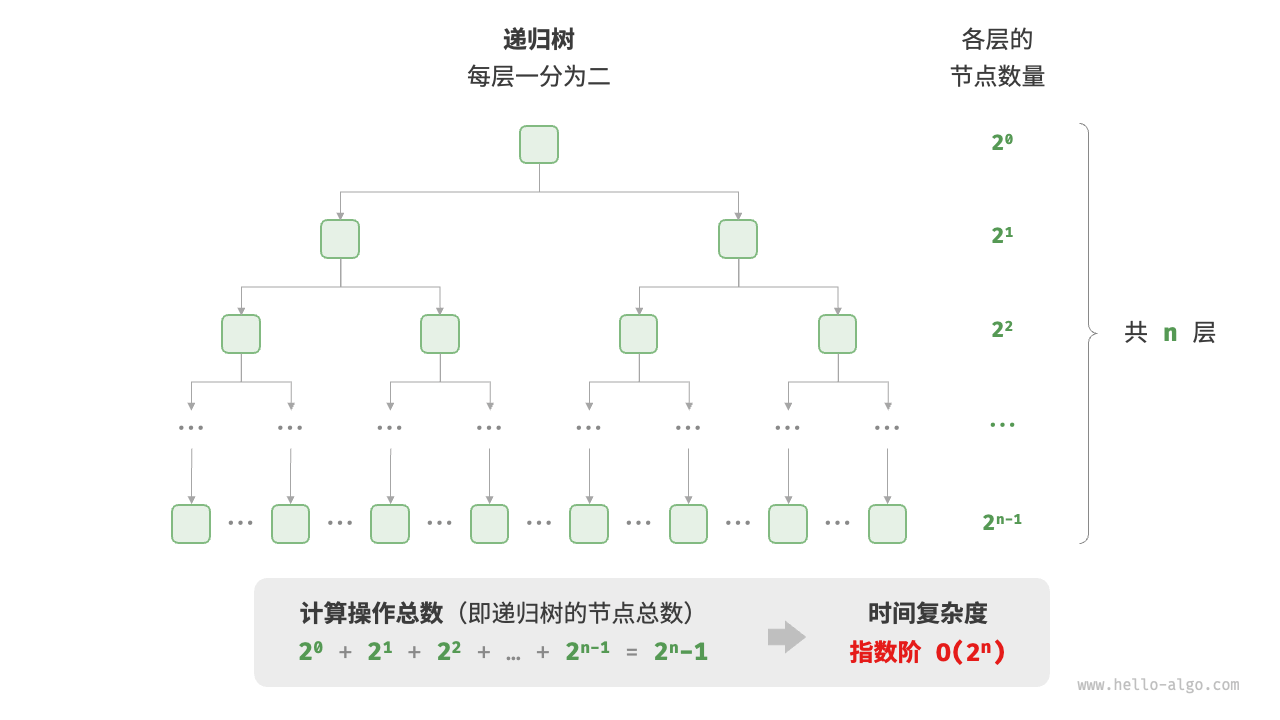

指数阶的时间复杂度

在实际算法中，指数阶常出现于递归函数中。例如在以下代码中，其递归地一分为二，经过 nn 次分裂后停止：

python
def exp_recur(n: int) -> int:
    """指数阶（递归实现）"""
    if n == 1:
        return 1
    return exp_recur(n - 1) + exp_recur(n - 1) + 1

建议

指数阶增长非常迅速，在穷举法（暴力搜索、回溯等）中比较常见。对于数据规模较大的问题，指数阶是不可接受的，通常需要使用动态规划或贪心算法等来解决。

对数阶 ​

与指数阶相反，对数阶反映了“每轮缩减到一半”的情况。设输入数据大小为 nn ，由于每轮缩减到一半，因此循环次数是 log2nlog_{2}^{n} ，即 2n2^n 的反函数。以下代码模拟了“每轮缩减到一半”的过程，时间复杂度为 O(log2n)O(log_{2}^{n}) ，由于对数的底数 22 可以在不影响复杂度的前提下转换，因此通常会省略对数的底数，直接简记为 O(logn)O(logn)：

python
def logarithmic(n: int) -> int:
    """对数阶（循环实现）"""
    count = 0
    while n > 1:
        n = n / 2
        count += 1
    return count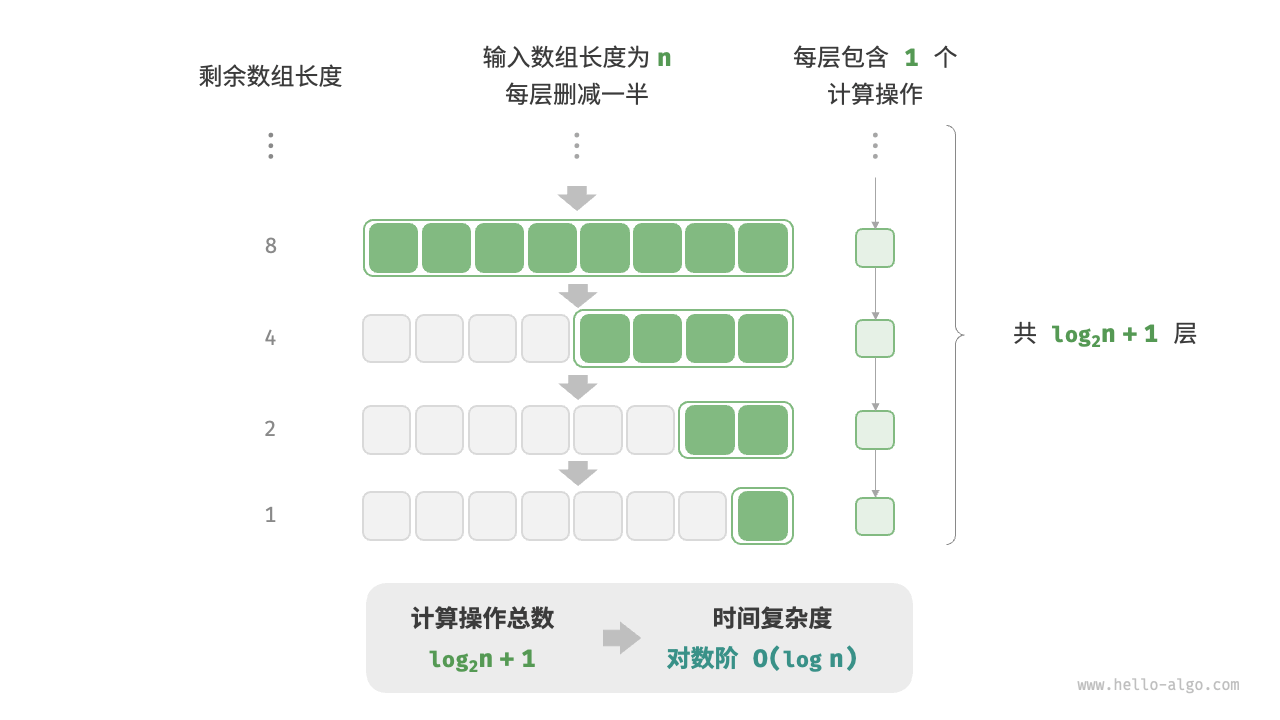

对数阶的时间复杂度

建议

对数阶常出现于基于分治策略的算法中，体现了“一分为多”和“化繁为简”的算法思想。它增长缓慢，是仅次于常数阶的理想的时间复杂度。

线性对数阶 ​

线性对数阶常出现于嵌套循环中，两层循环的时间复杂度分别为 O(logn)O(log^n) 和 O(n)O(n) 。相关代码如下：

python
def linear_log_recur(n: int) -> int:
    """线性对数阶"""
    if n <= 1:
        return 1
    count: int = linear_log_recur(n // 2) + linear_log_recur(n // 2)
    for _ in range(n):
        count += 1
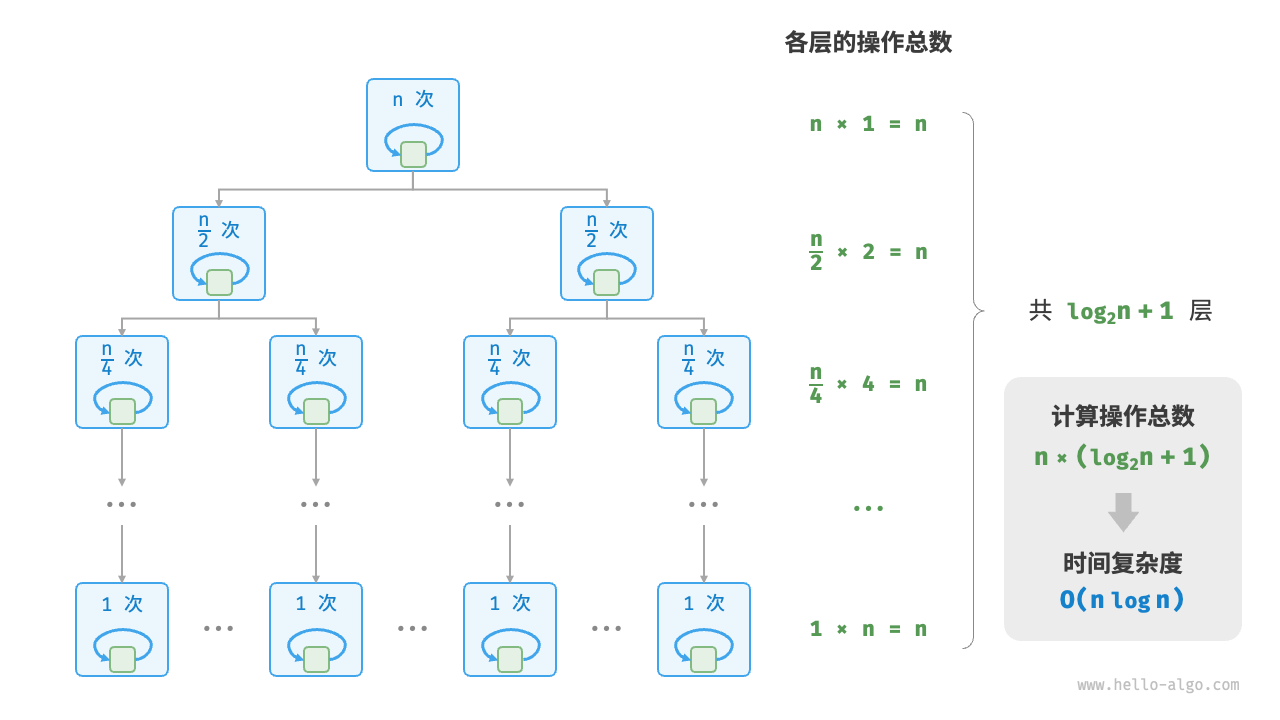
    return count

下图展示了线性对数阶的生成方式。二叉树的每一层的操作总数都为 nn ，树共有 log2n+1log_{2}^{n}+1 层，因此时间复杂度为 O(nlogn)O(nlogn) 。

线性对数阶的时间复杂度

建议

主流排序算法的时间复杂度通常为 O(nlog⁡n) ，例如快速排序、归并排序、堆排序等。

阶乘阶 ​

阶乘阶对应数学上的“全排列”问题。给定 nn 个互不重复的元素，求其所有可能的排列方案，方案数量为：

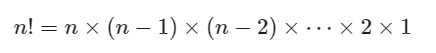
image-20240516163735245

阶乘通常使用递归实现。如下图和以下代码所示，第一层分裂出 nn 个，第二层分裂出 n−1 个，以此类推，直至第 nn 层时停止分裂：

python
def factorial_recur(n: int) -> int:
    """阶乘阶（递归实现）"""
    if n == 0:
        return 1
    count = 0
    # 从 1 个分裂出 n 个
    for _ in range(n):
        count += factorial_recur(n - 1)
    return count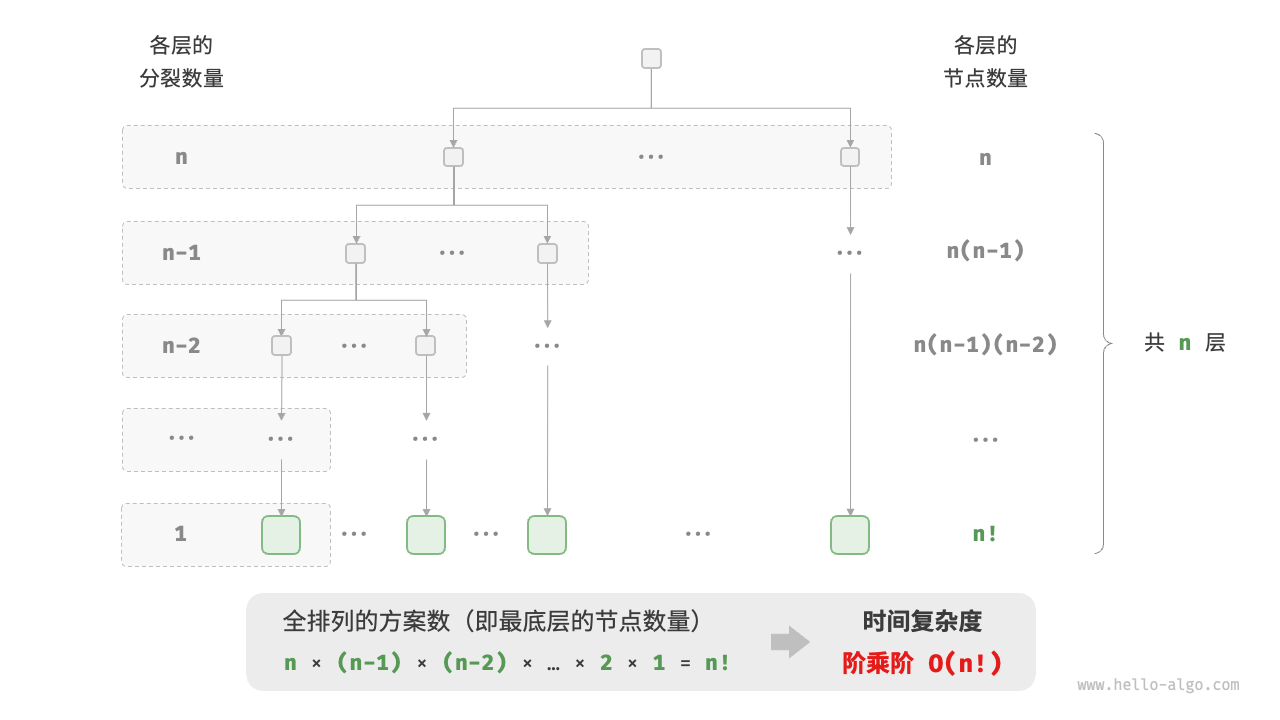

阶乘阶的时间复杂度

警告

请注意，因为当 n>=4n>=4 时恒有 n!>2nn!>2^n ，所以阶乘阶比指数阶增长得更快，在 nn 较大时也是不可接受的。

平均效率 ​

算法的时间效率往往不是固定的，而是与输入数据的分布有关。假设输入一个长度为 nn 的数组 nums ，其中 nums 由从 11 至 nn 的数字组成，每个数字只出现一次；但元素顺序是随机打乱的，任务目标是返回元素 11 的索引。我们可以得出以下结论：

  • 当 nums = [?, ?, ..., 1] ，即当末尾元素是 11 时，需要完整遍历数组，达到最差时间复杂度 O(n)O(n) 。
  • 当 nums = [1, ?, ?, ...] ，即当首个元素为 1 时，无论数组多长都不需要继续遍历，达到最佳时间复杂度 O(1)O(1) 。
python
def random_numbers(n: int) -> list[int]:
    """生成一个数组，元素为: 1, 2, ..., n ，顺序被打乱"""
    # 生成数组 nums =: 1, 2, 3, ..., n
    nums = [i for i in range(1, n + 1)]
    # 随机打乱数组元素
    random.shuffle(nums)
    return nums

def find_one(nums: list[int]) -> int:
    """查找数组 nums 中数字 1 所在索引"""
    for i in range(len(nums)):
        # 当元素 1 在数组头部时，达到最佳时间复杂度 O(1)
        # 当元素 1 在数组尾部时，达到最差时间复杂度 O(n)
        if nums[i] == 1:
            return i
    return -1

从上述示例可以看出，最差时间复杂度和最佳时间复杂度只出现于“特殊的数据分布”，这些情况的出现概率可能很小，并不能真实地反映算法运行效率。相比之下，平均时间复杂度可以体现算法在随机输入数据下的运行效率。上述示例中，由于输入数组是被打乱的，因此元素 1 出现在任意索引的概率都是相等的，那么算法的平均循环次数就是数组长度的一半 n/2n/2 ，平均时间复杂度为 O(n/2)O(n/2) 。

不过对于较为复杂的算法，计算平均时间复杂度往往比较困难，因为很难分析出在数据分布下的整体数学期望。所以在实际中，我们通常使用最差时间复杂度作为算法效率的评判标准，因为它给出了一个效率安全值，让我们可以放心地使用算法。

空间复杂度 ​

空间复杂度（space complexity）用于衡量算法占用内存空间随着数据量变大时的增长趋势。这个概念与时间复杂度非常类似，只需将“运行时间”替换为“占用内存空间”。

算法在运行过程中使用的内存空间主要包括以下几种：

  • 输入空间：用于存储算法的输入数据。
  • 暂存空间：用于存储算法在运行过程中的变量、对象、函数上下文等数据。
    • 暂存数据：用于保存算法运行过程中的各种常量、变量、对象等。
    • 栈帧空间：用于保存调用函数的上下文数据。系统在每次调用函数时都会在栈顶部创建一个栈帧，函数返回后，栈帧空间会被释放。
    • 指令空间：用于保存编译后的程序指令，在实际统计中通常忽略不计。
  • 输出空间：用于存储算法的输出数据。

在分析一段程序的空间复杂度时，我们通常统计暂存数据、栈帧空间和输出数据三部分，如下图所示：

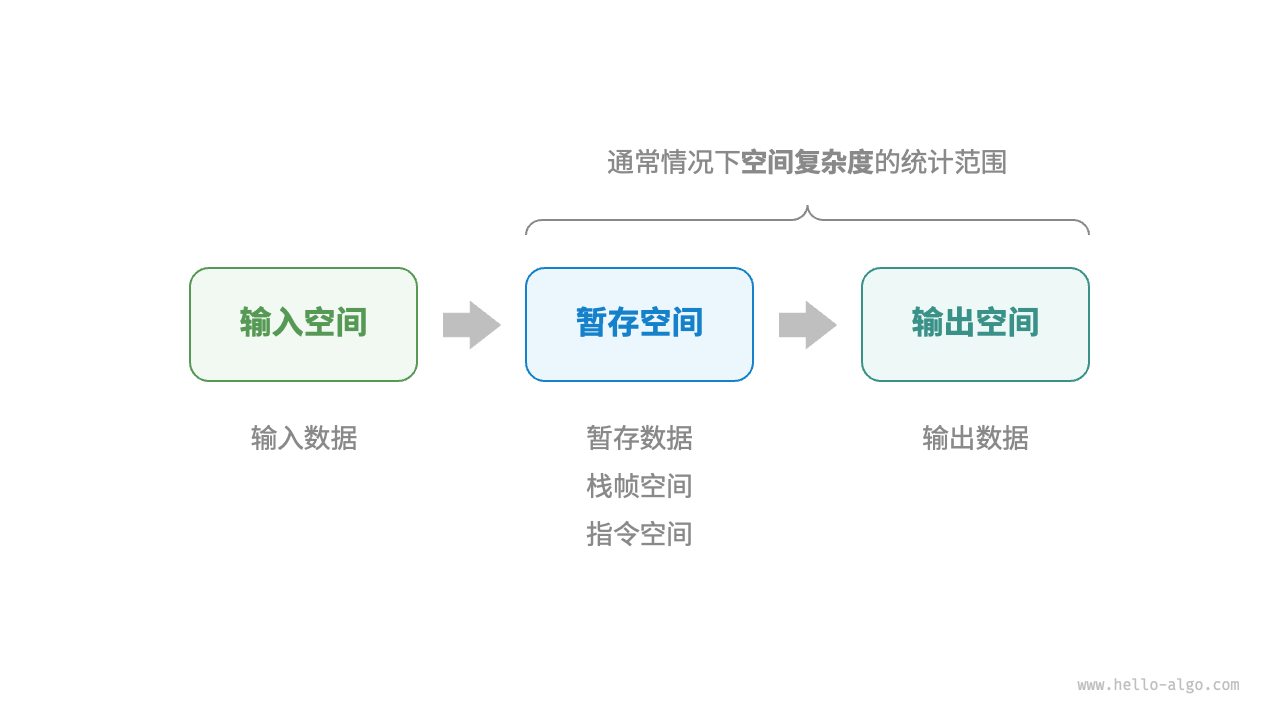
算法使用的相关空间

相关代码如下：

python
class Node:
    """类"""
    def __init__(self, x: int):
        self.val: int = x              # 节点值
        self.next: Node | None = None  # 指向下一节点的引用

def function() -> int:
    """函数"""
    # 执行某些操作...
    return 0

def algorithm(n) -> int:  # 输入数据
    A = 0                 # 暂存数据（常量，一般用大写字母表示）
    b = 0                 # 暂存数据（变量）
    node = Node(0)        # 暂存数据（对象）
    c = function()        # 栈帧空间（调用函数）
    return A + b + c      # 输出数据

推算方法 ​

空间复杂度的推算方法与时间复杂度大致相同，只需将统计对象从“操作数量”转为“使用空间大小”。而与时间复杂度不同的是，我们通常只关注最差空间复杂度。这是因为内存空间是一项硬性要求，我们必须确保在所有输入数据下都有足够的内存空间预留。观察以下代码，最差空间复杂度中的“最差”有两层含义：

  1. 以最差输入数据为准：当 n<10n<10 时，空间复杂度为 O(1)O(1) ；但当 n>10n>10 时，初始化的数组 nums 占用 O(n)O(n) 空间，因此最差空间复杂度为 O(n)O(n) 。
  2. 以算法运行中的峰值内存为准：例如，程序在执行最后一行之前，占用 O(1)O(1) 空间；当初始化数组 nums 时，程序占用 O(n)O(n) 空间，因此最差空间复杂度为 O(n)O(n) 。
python
def algorithm(n: int):
    a = 0               # O(1)
    b = [0] * 10000     # O(1)
    if n > 10:
        nums = [0] * n  # O(n)

在递归函数中，需要注意统计栈帧空间。观察以下代码：

python
def function() -> int:
    # 执行某些操作
    return 0

def loop(n: int):
    """循环的空间复杂度为 O(1)"""
    for _ in range(n):
        function()

def recur(n: int):
    """递归的空间复杂度为 O(n)"""
    if n == 1:
        return
    return recur(n - 1)

函数 loop() 和 recur() 的时间复杂度都为 O(n)O(n) ，但空间复杂度不同。

  • 函数 loop() 在循环中调用了 nn 次 function() ，每轮中的 function() 都返回并释放了栈帧空间，因此空间复杂度仍为 O(1)O(1) 。
  • 递归函数 recur() 在运行过程中会同时存在 nn 个未返回的 recur() ，从而占用 O(n)O(n) 的栈帧空间。

常见类型 ​

设输入数据大小为 nn ，图 2-16 展示了常见的空间复杂度类型（从低到高排列）。

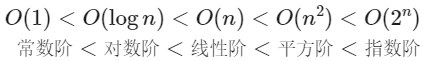
image-20240516171104087

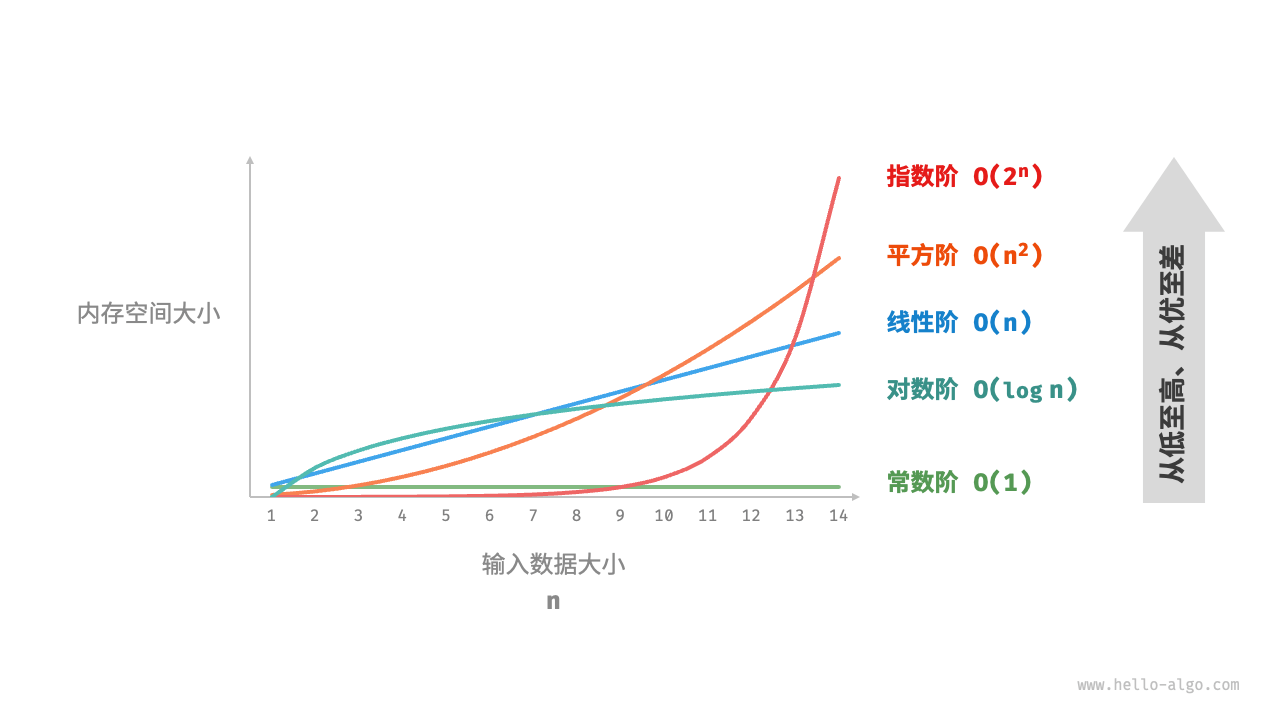
常见的空间复杂度类型

常数阶 ​

常数阶常见于数量与输入数据大小 nn 无关的常量、变量、对象。需要注意的是，在循环中初始化变量或调用函数而占用的内存，在进入下一循环后就会被释放，因此不会累积占用空间，空间复杂度仍为 O(1)O(1) ：

python
def function() -> int:
    """函数"""
    # 执行某些操作
    return 0

def constant(n: int):
    """常数阶"""
    # 常量、变量、对象占用 O(1) 空间
    a = 0
    nums = [0] * 10000
    node = ListNode(0)
    # 循环中的变量占用 O(1) 空间
    for _ in range(n):
        c = 0
    # 循环中的函数占用 O(1) 空间
    for _ in range(n):
        function()

线性阶 ​

线性阶常见于元素数量与 nn 成正比的数组、链表、栈、队列等：

python
def linear(n: int):
    """线性阶"""
    # 长度为 n 的列表占用 O(n) 空间
    nums = [0] * n
    # 长度为 n 的哈希表占用 O(n) 空间
    hmap = dict[int, str]()
    for i in range(n):
        hmap[i] = str(i)

如下图所示，此函数的递归深度为 nn ，即同时存在 nn 个未返回的 linear_recur() 函数，使用 O(n)O(n) 大小的栈帧空间：

python
def linear_recur(n: int):
    """线性阶（递归实现）"""
    print("递归 n =", n)
    if n == 1:
        return
    linear_recur(n - 1)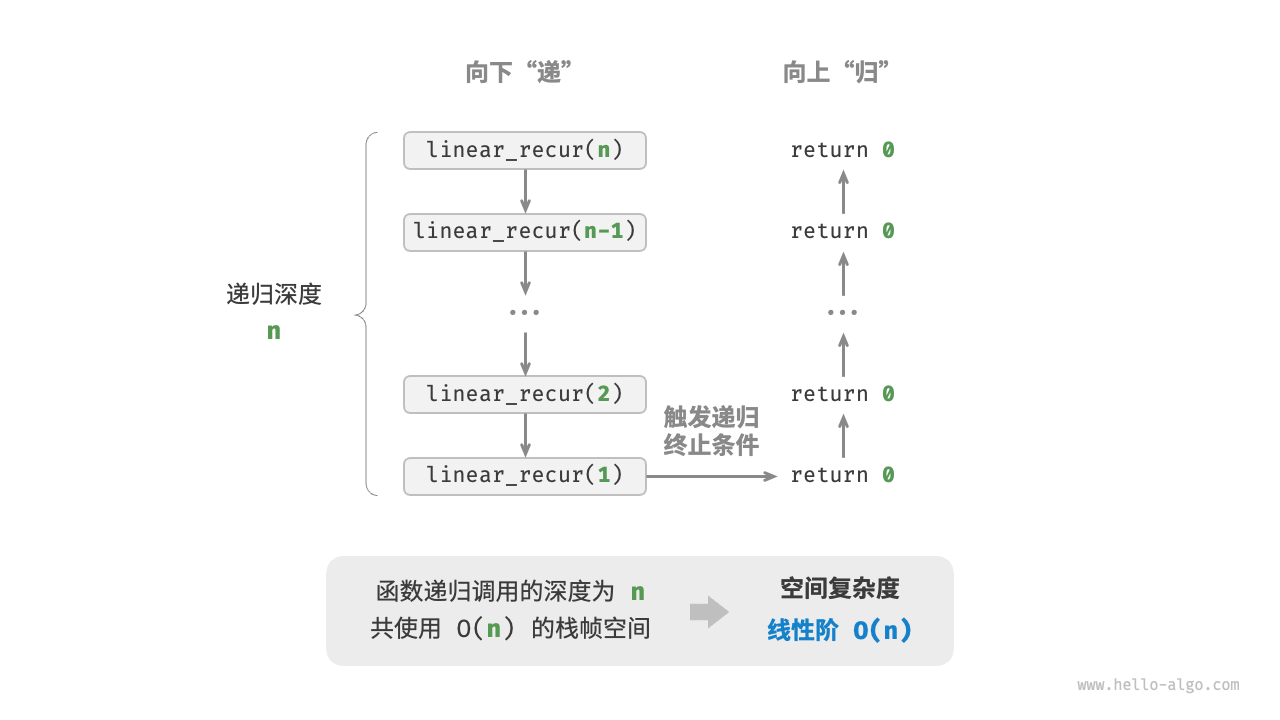

递归函数产生的线性阶空间复杂度

平方阶 ​

平方阶常见于矩阵和图，元素数量与 nn 成平方关系：

python
def quadratic(n: int):
    """平方阶"""
    # 二维列表占用 O(n^2) 空间
    num_matrix = [[0] * n for _ in range(n)]

如下图所示，该函数的递归深度为 nn ，在每个递归函数中都初始化了一个数组，长度分别为 nn、n−1n-1、…、22、11 ，平均长度为 n/2n/2 ，因此总体占用 O(n2)O(n^2) 空间：

python
def quadratic_recur(n: int) -> int:
    """平方阶（递归实现）"""
    if n <= 0:
        return 0
    # 数组 nums 长度为 n, n-1, ..., 2, 1
    nums = [0] * n
    return quadratic_recur(n - 1)

递归函数产生的平方阶空间复杂度

指数阶 ​

指数阶常见于二叉树。观察下图，层数为 nn 的“满二叉树”的节点数量为 2n−12^n-1 ，占用 O(2n)O(2n) 空间：

python
def build_tree(n: int) -> TreeNode | None:
    """指数阶（建立满二叉树）"""
    if n == 0:
        return None
    root = TreeNode(0)
    root.left = build_tree(n - 1)
    root.right = build_tree(n - 1)
    return root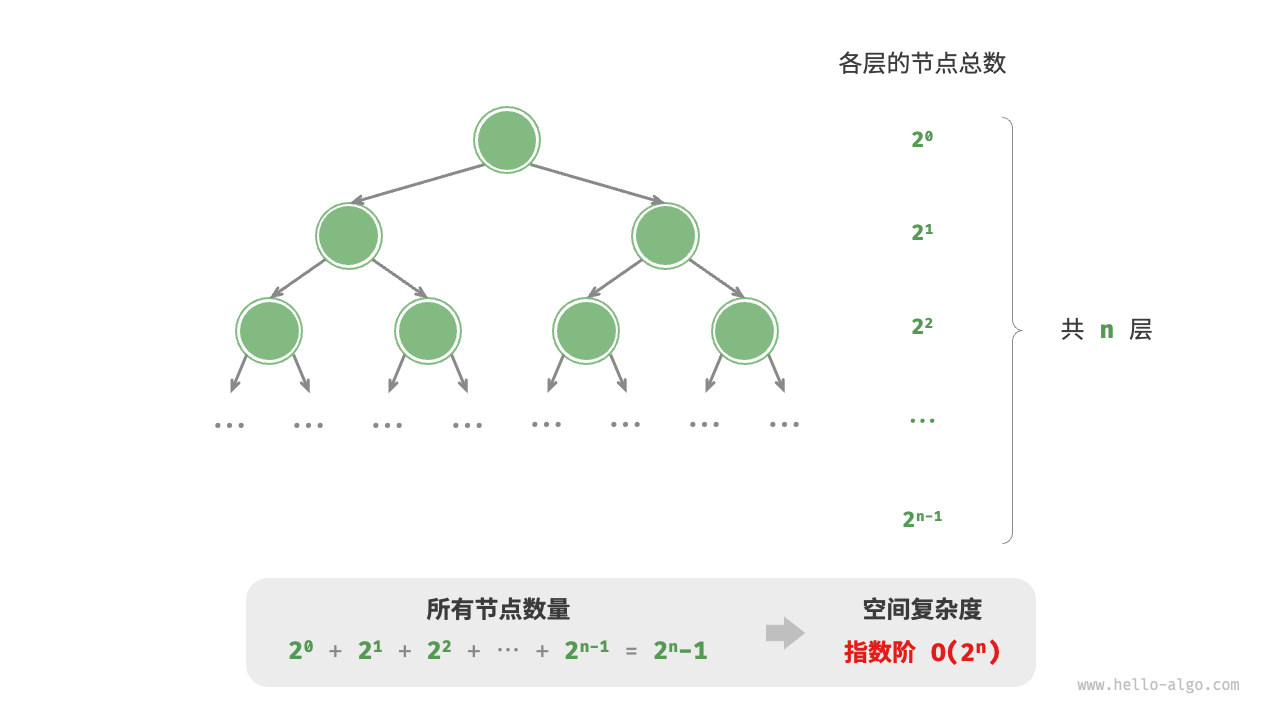

满二叉树产生的指数阶空间复杂度

对数阶 ​

对数阶常见于分治算法。例如归并排序，输入长度为 nn 的数组，每轮递归将数组从中点处划分为两半，形成高度为 lognlogn 的递归树，使用 O(logn)O(logn) 栈帧空间。再例如将数字转化为字符串，输入一个正整数 nn ，它的位数为 log10n+1log_{10}^{n}+1 ，即对应字符串长度为 log10n+1log_{10}^{n}+1 ，因此空间复杂度为 O(log10n+1)=O(logn)O(log_{10}^{n}+1)=O(logn) 。

权衡时间与空间 ​

理想情况下，我们希望算法的时间复杂度和空间复杂度都能达到最优。然而在实际情况中，同时优化时间复杂度和空间复杂度通常非常困难，它们之间更多通常是鱼和熊掌的关系。也就意味着，降低时间复杂度通常需要以提升空间复杂度为代价，反之亦然。我们将牺牲内存空间来提升算法运行速度的思路称为“以空间换时间”；反之，则称为“以时间换空间”。因此在计算机中有“时间和空间通常是不可调和的矛盾”这一说法。

选择哪种思路取决于我们更看重哪个方面。在大多数情况下，时间比空间更宝贵，而且现今的计算机硬件已经有了很大的进步，当空间不够的时候，我们可以用很低的成本去给计算机增加新的内存空间，因此“以空间换时间”通常是更常用的策略。当然，在数据量很大的情况下，控制空间复杂度也非常重要。但无论程序的算法多么的优秀，我们总是希望程序能尽快的给到我们结果，因此对时间的追求可能一直都是我们要孜孜不倦的去做的事情。