梯度下降
更新: 2025/2/24 字数: 0 字 时长: 0 分钟
前面我们讲过,深度学习模型优化的核心目标,就是要计算使损失函数取得最小值时的模型参数(自变量)的取值,但由于损失函数的复杂性和非凸性,直接找到全局最值点在实践中很难实现。所以在实际的深度学习中,我们会使用优化算法(如梯度下降)来找到损失函数的极值点(局部极小值),这通常也能达到足够好的模型优化效果。所以,本章节我们来深入学习人工智能中最原始、最基础、最核心的梯度下降算法。
数学原理
首先,我们来了解一下梯度(gradient)以及梯度下降的数学原理,这样才有利于进行后面的学习。
一元导数
一元导数指的是一元函数的导数(梯度),使用一个撇点符号 来表示某个一元函数的梯度。
以函数 为例,说明计算梯度的过程:求出函数 关于 的导数,结果是 ,它表示了 在任意点 上的瞬时变化率。
为了更好的理解梯度 ,我们画出函数 的二维图像,取函数上的某一点 坐标为 ,将点 投影到 坐标系上,得到点 在 位置上,具体如下图所示:
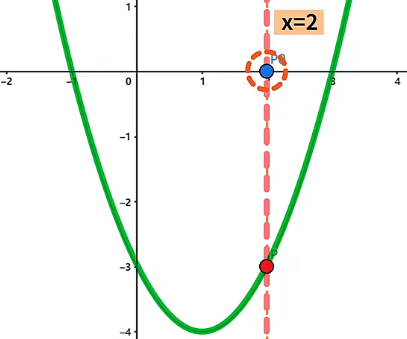
现在问题来了,假如点 可以沿 轴的正、负方向移动,那么它往哪个方向上移动会使得函数 的值减小呢?面对这个问题,我们可以根据 与 的大小关系进行判断,具体来说有如下三种情况:
- 在函数 上的某一点使得 , 那么该点沿 轴的正方向运动,会使得函数值变大,反之该点沿 轴的负方向运动,会使得函数值变小。例如点 坐标为 ,投影到 坐标系上的点 在 位置上,此时 ,因此点 沿 轴的负方向移动,会使得函数值变小。
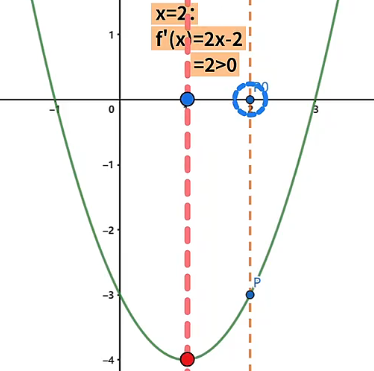
- 在函数 上的某一点使得 , 那么该点是函数的极值点,如果沿 轴正、负方向运动都使得函数值变大,则说明该点是函数的极小值点,反之沿 轴正、负方向运动都使得函数值变小,则说明该点是函数的极大值点。例如点 坐标为 ,投影到 坐标系上的点 在 位置上,此时 ,因此点 是函数的极值点,且点 沿 轴的正、负方向移动,都会使得函数的值变大,所以点 是函数的极小值点。
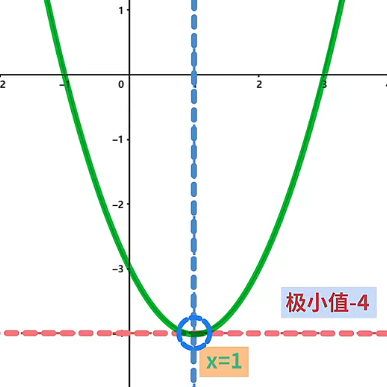
- 在函数 上的某一点使得 , 那么该点沿 轴的正方向运动,会使得函数值变小,反之该点沿 轴的负方向运动,会使得函数值变大。例如点 坐标为 ,投影到 坐标系上的点 在 位置上,此时 ,因此点 沿 轴的正方向移动,会使得函数的值变小。
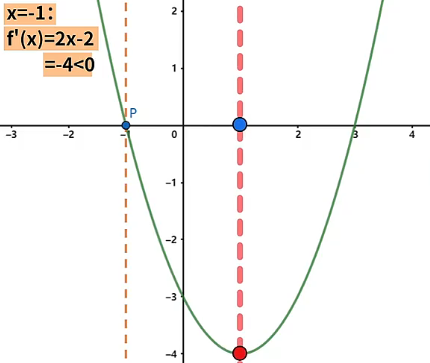
多元向量
多元向量指的是多元函数全部偏导数所构成的向量(梯度),使用倒三角符号 来表示某个多元函数的梯度。
以函数 为例,说明计算梯度向量的过程:求出函数 关于 和 的偏导数,结果分别是 和 ,这两个偏导数的组合就是函数 的梯度向量 ,它表示了 在任意点 上的变化方向和速率。
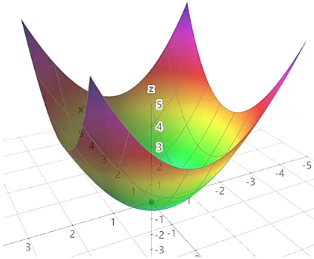
为了更好的理解梯度向量 ,我们画出函数 的三维图像,下面灰色部分就是 平面坐标系,也就是函数 中自变量 和 的取值范围。在函数 中,修改函数自变量 和 的取值,就会导致函数值发生变化。对应到函数图像中,其实就是点在 平面坐标系上运动,进而导致该点对应的函数值发生变化。现在我们设 平面坐标系上坐标为 的点为点 ,那么 的函数值就是 ,将其对应到三维函数图像中就得到坐标为 的一点,具体如下图所示:
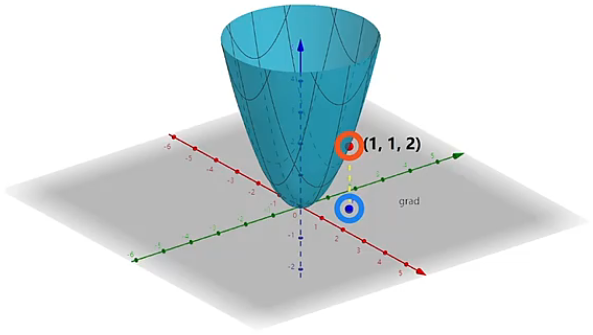
现在问题来了,假如点 可以在 平面坐标系上往任意方向移动 个单位距离,那么它往哪个方向上移动可以使函数 的值增大或减小的最快呢?面对这个问题,我们就要用到函数的梯度性质了,具体如下:
- 函数上的某一点,如果沿着函数梯度的正方向运动,对应的函数值增加的最快。
- 函数上的某一点,如果沿着函数梯度的反方向运动,对应的函数值减小的最快。
如何来理解函数的梯度性质呢?在 平面坐标系上的点 就表示了函数的自变量的取值,将点 的坐标 带入到函数的梯度向量 ,得到点 的正梯度为 ,相反的负梯度就为 ,也就意味着点 从坐标 向着坐标 运动,对应的函数值增加的最快,相反点 从坐标 向着坐标 运动,对应的函数值减小的最快。那么如何来证明这个结论呢?我们令点 向 、 或 三个不同的方向运动 个单位距离,分别到达 、、 三个不同的点,比较 、、 这三个点的函数值相比 点的函数值变化,就可以看出沿着哪个方向运动函数值变化的最快,具体情况如下:
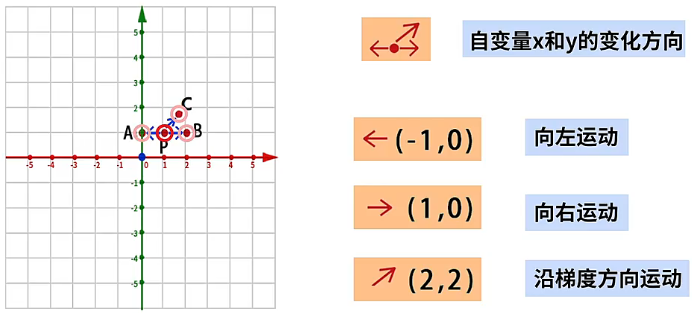
坐标为 的点 沿着向量 的方向移动 个单位到达坐标为 的 点,那么 点的函数值为 ,相比 点的函数值 减小了 。
坐标为 的点 沿着向量 的方向移动 个单位到达坐标为 的 点,那么 点的函数值为 ,相比 点的函数值 增大了 。
坐标为 的点 沿着向量 的方向移动 个单位到达坐标为 的 点,为了方便计算我们将 点的坐标等同为近似值 ,那么 点的函数值为 ,相比 点的函数值 增大了 。
从这个例子中可以看到,同样是移动 个单位长度,如果函数上的某个点,沿着该点的梯度方向移动,函数增长的最为迅猛。相应的,如果沿着梯度的反方向运动,函数的值减小的最快。这就是为什么梯度下降算法需要沿着梯度的反方向来修改自变量的取值,目的就是要使函数值以最快的速度减小,从而找到目标函数的极小值。
一元函数求极值
这里我们会基于一元函数求极值问题,来说明梯度下降算法的原理和执行过程。
使用方式
例如,求解一元函数 取得极小值时 的取值,有如下两种方法来计算:
- 方法一:使用求导数的数学方法,令一元函数 的导数 ,求的该函数在 处,取得极小值 。

- 方法二:使用梯度下降算法,通过循环迭代找到该函数的极小值点。具体包含如下六个步骤。
- 随机设置自变量的初始值,也就是设置自变量的初始位置。
- 计算当前所在位置的梯度。
- 计算运动的步长。
- 沿梯度反方向运动计算的步长。
- 重复 2、3、4 步骤,不断地调整自变量所在的位置。
- 经过足够多的迭代后,计算的运动步长会趋近于 ,此时自变量所在位置就是函数的极小值点。
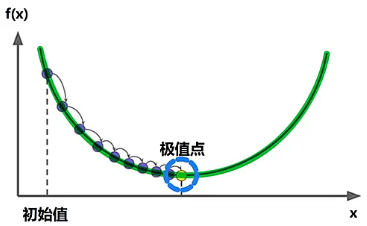
详细说明
这里我们详细说明梯度下降算法的执行过程,具体如下:
- 随机为自变量 ,设置一个初始值。例如,令 。
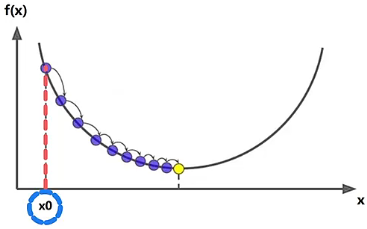
- 计算 位置的梯度,也就是计算出 的导数 后,将 带入到导函数 中,得到 ,继而得到 应该向哪个方向运动。

- 计算运动一小步的长度,这个长度为 ,对应图中两条虚线之间的距离,这个 是一个常量,被称为学习速率,用来控制这一小步到底有多长。
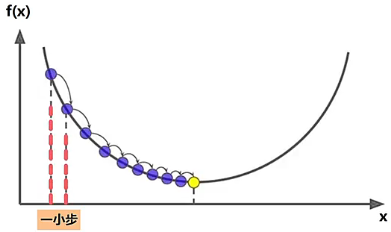
- 令 沿梯度的反方向运动,也就是让 从 的位置沿着 的负方向运动一小步到达 的位置。这一小步的长度我们已经计算出是 ,因此运动后的新位置 。此时,我们就完成了一轮的梯度下降算法。
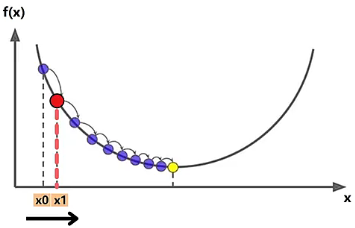
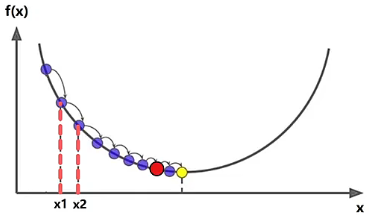
- 到达 的位置之后,需要重新计算 位置的梯度的值 ,然后计算一小步长度 ,再继续沿着 的负方向运动一小步到达 的位置。按照这样的方式,重复 2、3、4步,一小步一小步的不断调整自变量 的位置。
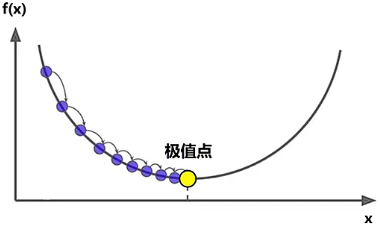
- 当自变量 走了足够多的一小步后,也就是经过足够多的迭代次数, 会趋近于 ,这就会使得自变量 移动的一小步趋近于 ,也就是图中黄色标记的位置,这里 将无法再向前移动,此时自变量 的值就是我们要求的结果。
举例说明
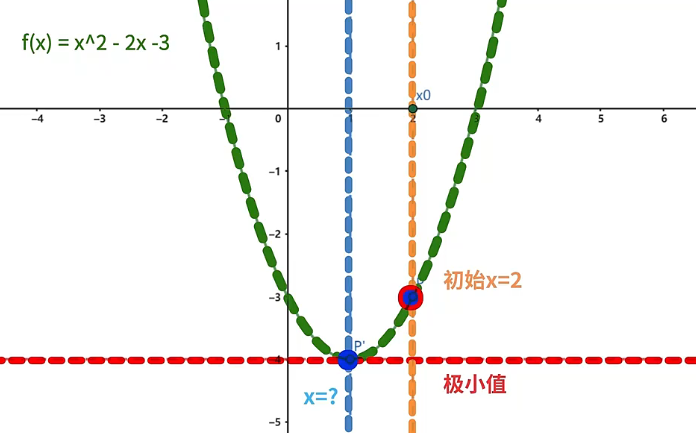
以一元函数 为例,画出图像,设自变量 的初始值为 ,该位置在极值点的右侧,计算该位置的梯度 ,因此自变量 沿 轴的负方向移动会使得函数值变小。
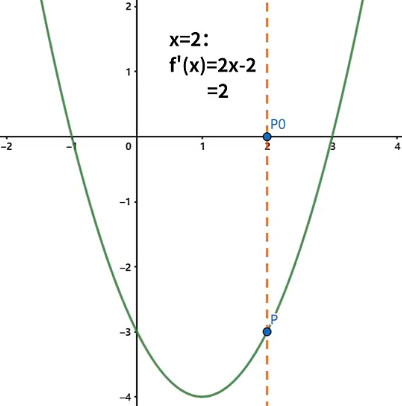
这里,我们让自变量 沿 轴的负方向移动一小步,然后再重新对自变量 赋值。为了看清变化,我们将坐标系的刻度放大,将坐标系的刻度定位 ,设置迭代速率 ,因此自变量 移动一小步的距离是 ,自变量 新的值为 。
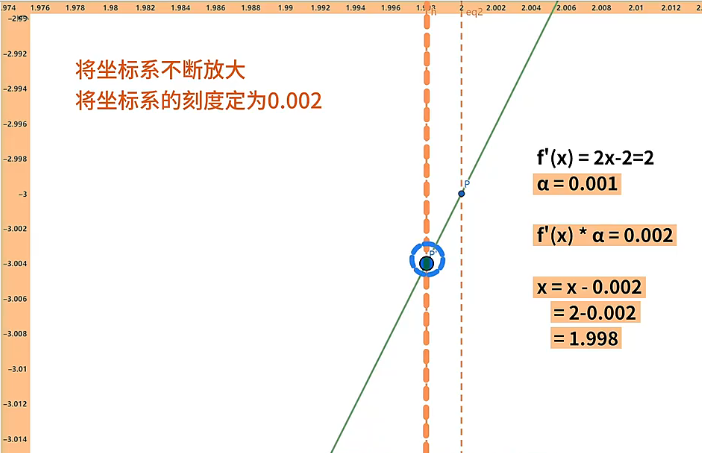
当自变量 到达新位置 后,需要重新计算自变量 在该位置的梯度,计算过程为 ,因此自变量 移动一小步的距离是 ,自变量 新的值为 。随着迭代次数的不断增加,自变量 会不断向左侧的极值点运动,函数的导数 也会不断变小。当自变量 到达函数的极值点时,函数的导数 趋近于 ,此时自变量 到达 的位置,我们就求出了函数取得的极小值。
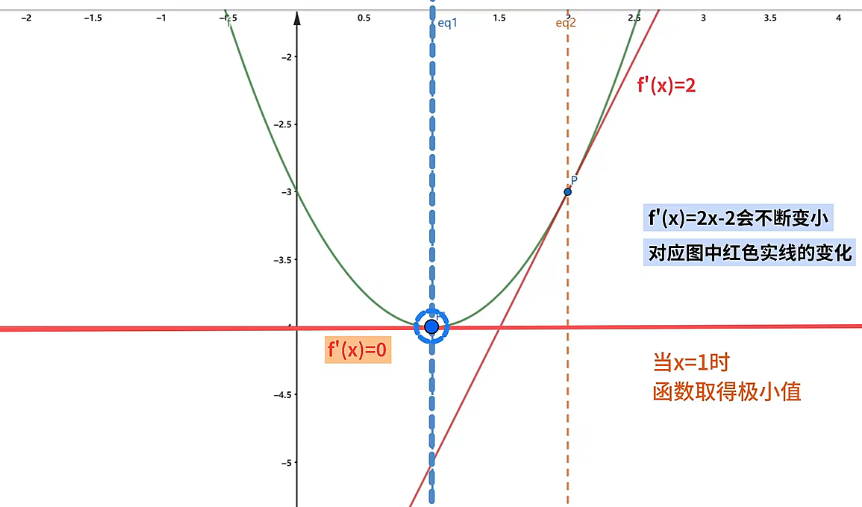
提醒
函数的导数 的变化,对应了图中红色切线斜率的变化。
代码实现
最后来看使用梯度下降求二次函数 极值的代码实现,具体如下:
x = 2 # 初始化
alpha = 0.001 # 迭代速率
# 先将迭代次数设置为一个较小的值,用来调试程序
iteration_num = 10000 # 迭代次数
# 进入迭代循环
for i in range(1, iteration_num + 1):
gradient = 2.0 * x - 2 # 计算梯度
step = alpha * gradient # 计算一小步
x = x - step # 进行梯度下降
# 打印调试信息
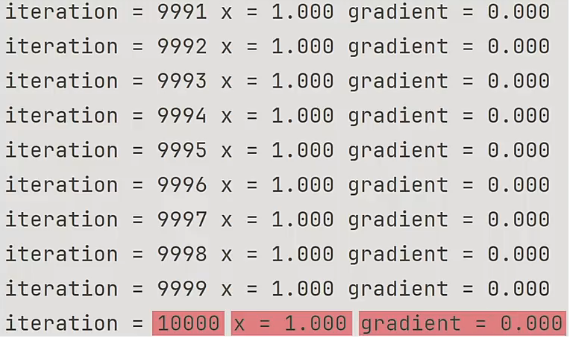
print(f"iteration = {i} x = {x:.3f} gradient = {gradient:.3f}")在前 10 次的迭代中,每次迭代自变量 都会减小一点,随着 的变化,梯度 gradient 也会不断变小,这是因为越靠近极值点,梯度的值会越小。
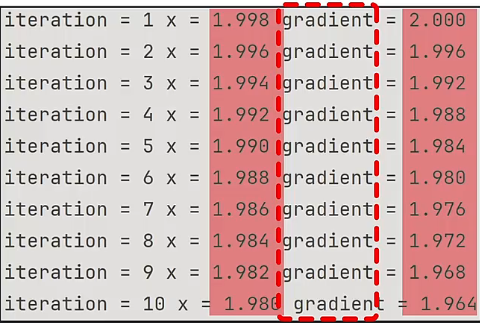
经过 10000 次的迭代后,自变量 在 的位置,梯度 gradient 趋近于 ,函数 就收敛在这个位置,这就是最终的结果。
多元函数求极值
这里我们会基于二元函数求极值问题,详细说明梯度下降算法的原理和执行过程。
求解方法
例如,求解二元函数 取得极小值时 和 的取值,有如下两种方法来计算:
- 方法一:使用求偏导数的数学方法,求的该函数在 、 处,取得极小值 。
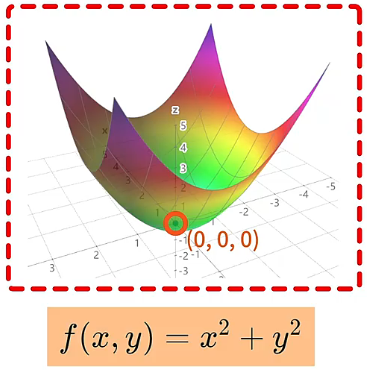
- 方法二:使用梯度下降算法,通过循环迭代找到该函数的极小值点。具体就是对函数 执行梯度下降算法后,算法会不断调整目标函数中的参数值,使得目标函数的值不断变小,最后求出目标函数在在 、 处,取得极小值 。

详细过程
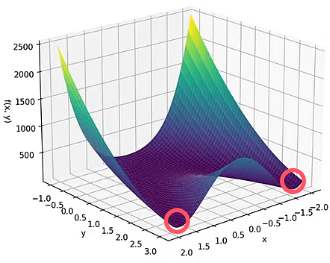
设某个随机的二元函数是 ,其中 和 是自变量,函数有多个深蓝色标记的极小值点。执行梯度下降算法具体的过程如下:
- 首先对自变量 和 进行初始化,我们可以随意的设置自变量的初始值。例如,设置为 、,对应点 的位置。
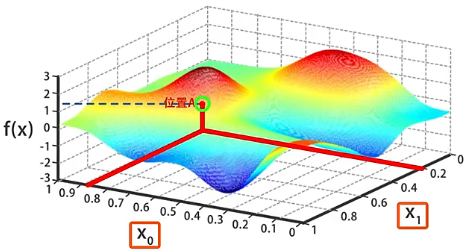
- 计算出位置 处的梯度,沿着梯度的反方向走一小步(也就是沿着梯度的反方向略微的修改 和 的值),到达函数值 更小的位置 。
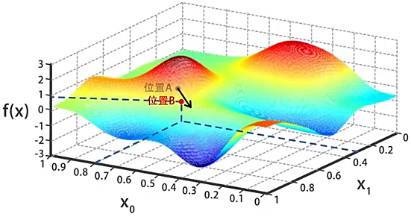
- 同上一步流程一样,在位置 处计算出梯度,沿着梯度的反方向走一小步(也就是沿着梯度的反方向略微的修改 和 的值),到达函数值 更小的位置 。
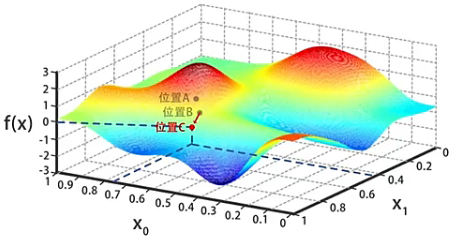
- 不断重复上一步流程,一点一点的调整 和 的值使 逐渐变小,直到 到达图中三角标记的局部最小值,此处求得 、,这两个值会作为算法的结果返回。
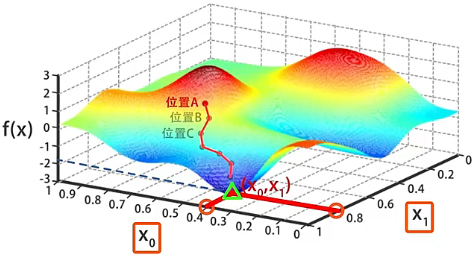
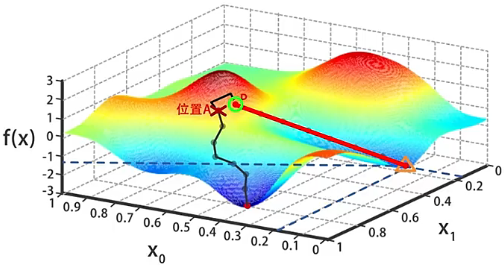
需要注意的是,上图中三角标记的不是全局最小值,而是从位置 出发,通过梯度下降一点一点找到的局部最小值。如果一开始初始化 和 的时候,我们选择了位置 旁边的某个点 ,在这个基础上进行梯度下降搜索,很可能会到达图中三角标记的另一个局部最优解。
代码实现
这里我们会用 Python 实现一个求函数 极小值的梯度下降算法。在运行梯度下降算法前,需要求出该函数在任意一点的梯度向量 ,其计算流程在上面的多元向量中有,这里不再赘述,直接给结果 ,具体的梯度下降算法代码实现如下:运行程序可以看到,经过 100 轮的迭代后,我们找到了 、 时,函数 取得极小值 。
x = 1.1 # 首先随意设置自变量x和y的初始值
y = 2.1
n = 100 # 迭代轮数
alpha = 0.05 # 迭代速率,alpha用于控制“一小步”的大小
for i in range(1, n + 1): # 梯度下降是一个迭代的过程,对应这里的for循环
# 在循环中,我们会一步一步的调整自变量的取值,让函数不断减小
gx = x * 2 # 自变量x的梯度值
gy = y * 2 # 自变量y的梯度值
# gx和gy用于控制迭代的方向
x = x - alpha * gx # x方向的一小步
y = y - alpha * gy # y方向的一小步
# 计算过后,自变量(x, y),就沿着负梯度的方向,移动了一小步
print(f'After {i} iterations, ' # 迭代轮数i
f'x = {x:.3f}, ' # 自变量x
f'y = {y:.3f}, ' # 自变量y
f'f(x, y) = {x**2 + y**2:.3f}') # 函数值f(x,y)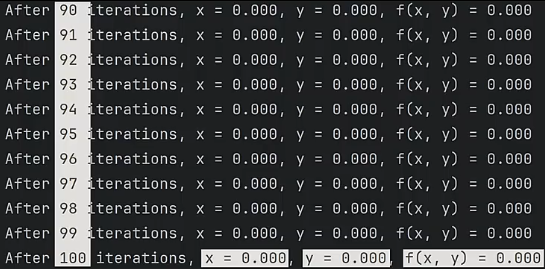
算法总结
经过上面的流程学习和代码实现,到这里我们就能总结得到,梯度下降算法肯定能找到目标函数的某个局部最小值,但这个局部最小值不一定就是目标函数的全局最小值,这与目标函数 本身的数学性质有关。
- 如果 是凸函数,那么梯度下降算法可以保证求出全局最小值。例如,函数 ,我们肯定可以通过梯度下降算法求得 、 处的最优解。
- 如果 是非凸函数,那么梯度下降算法就只能求出某个局部最小值。例如,函数 ,我们可能会求出前方的最小值,也可能求出后方的最小值,这个与最开始的初始位置有关。
迭代速率
上面我们在使用梯度下降对参数 进行迭代时,使用了常量 来控制以多大的幅度来更新参数 ,从而控制迭代的速度,而这个常量 就是迭代速率,也叫学习速率(Learning Rate)。在梯度下降中,定义合适的迭代速率,可以让模型的迭代事半功倍,使得用更少的迭代次数,找到最优解。
定义取值
在每次进行梯度下降时,都会使用公式 对自变量 进行更新,其中 的取值对应如下三种情况:
- 如果迭代速率 过小,就会导致 的值过小,那么自变量 每次更新几乎都不会有什么变化,这会导致需要更多的迭代轮数,才能找到最优解。或者甚至经过几百万次的迭代,都无法找到最优解。
- 如果迭代速率 适中,自变量 每次更新都会到达一个新的并且更靠近最低点的位置。这样经过一定次数的迭代后,自变量 就能逼近甚至找到最优解,进而完成收敛。
- 如果迭代速率 过大,有可能导致自变量 越过最低点,并且更加远离最低点,最终导致迭代永远无法收敛,无法找到最优解。
详细过程
上述 取值的三种情况,前两种相信大家都很好理解,至于第三种迭代速率 过大的情况,我们具体举一个例子来说明。设函数 ,求 取得极小值时 的取值,计算过程如下:
- 首先,令 (这是一个非常大的值),初始位置为 。
- 第一步,计算 位置的梯度 ,具体为 。
- 第二步,计算一小步,也就是使 向负方向移动 的长度,具体为 。
- 第三步,移动 ,移动后到达了 的位置,这里就已经越过了 的极值点了。
- 到这里,如果继续迭代,就需要计算新位置 的导数。
- 第四步,计算 位置的梯度 ,具体为 。
- 第五步,计算一小步,具体为 。
- 第六步,移动 ,移动后到达了 的位置,这里就距离 的极值点已经非常远了。
可以看到,在迭代速率 过大的情况下,随着迭代的进行, 就会离极值点越来越远,导致迭代永远都不会收敛。
代码实现
另外上述 取值的三种情况,我们可以通过代码来实现。设函数 ,求 取得极小值时 的取值,代码如下:
# 函数的梯度(导数)
def f_grad(x):
# 目标函数是x**2,该函数的梯度(导数)就是2*x
return 2*x
# 梯度下降(eta迭代速率,f_grad梯度函数)
def gd(eta, f_grad):
# 初始值
x = 10.0
# 经历10轮迭代
for i in range(10):
# 上一轮的值减去迭代速率乘以梯度值
x -= eta * f_grad(x)
# 输出10轮迭代后x的值
print(f'{x:f}')
# 迭代速率太小
gd(0.05, f_grad) # 输出:3.486784。注释:10轮迭代后,距离极值点还有段距离。
# 迭代速率适中
gd(0.2, f_grad) # 输出:0.060466。注释:10轮迭代后,距离极值点十分近了。
# 迭代速率太大
gd(1.1, f_grad) # 输出:61.917364。注释:10轮迭代后,距离极值点更加远了。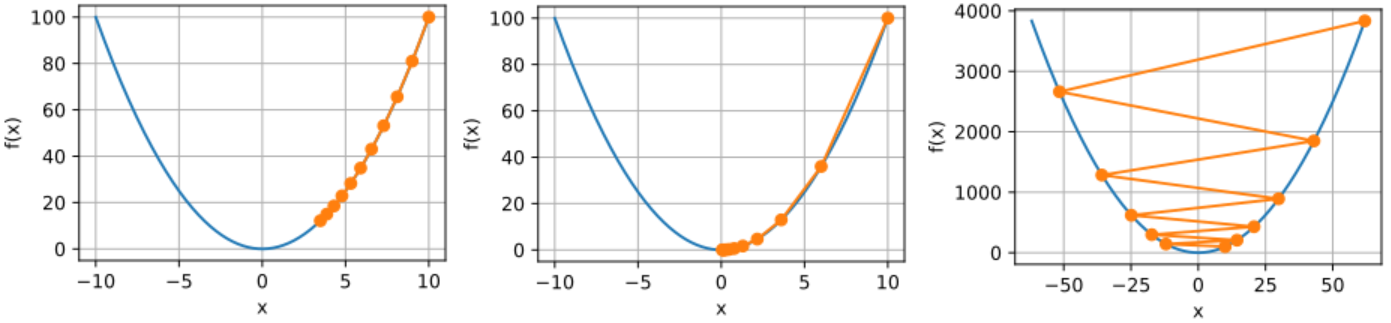
**上面我们选择了一个简单的二次函数,通过选择合适的迭代速率就能快速逼近全局最优解,也就是所有情况下的最优解。但如果我们选择了非凸函数,并且选择了过大的迭代速率,我们最终可能只会得到一个局部最优解,也就部分情况下的最优解。**下面的例子说明了过大的迭代速率如何导致较差的局部最小值:
import torch
# 非凸函数f
c = torch.tensor(0.15 * np.pi)
f = x * torch.cos(c * x)
# 函数的梯度(导数)
def f_grad(x):
# 假设目标函数是f,该函数的梯度(导数)如下
return torch.cos(c * x) - c * x * torch.sin(c * x)
# 进行梯度下降(eta迭代速率,f_grad梯度函数)
def gd(eta, f_grad):
# 初始值
x = 10.0
# 经历10轮迭代
for i in range(10):
# 上一轮的值减去迭代速率乘以梯度值
x -= eta * f_grad(x)
# 输出10轮迭代后的值
print(f'{x:f}')
# 迭代速率太大
gd(2, f_grad) # 输出:-1.528166。注释:10轮迭代后,得到了一个较差的局部最优解。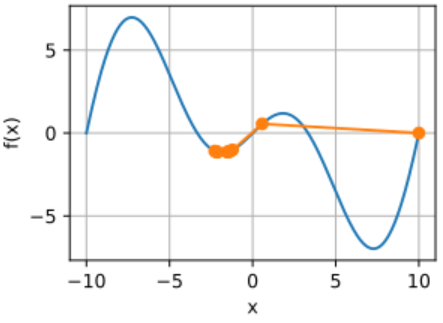
取值建议
在实际应用梯度下降时,迭代速率 可以多尝试一些取值,一般的取值范围在 到 之间。至于如何选择,这与目标函数 本身的情况有关:
- 如果 比较平缓光滑,迭代速率 可以设置大一些。
- 如果 在某些区域的导数变化剧烈,迭代速率 就要小一些,使迭代更稳定。
疑问解答
上面我们介绍了迭代速率 是一个常量,但有同学会觉得,随着迭代的进行,迭代速率 应该越来小,这样才可以保证移动的步子越来越小?
答:仔细研究梯度下降公式 会发现随着 向极值点移动,对应位置的梯度 会不断减小,因此 移动的距离 也会自动变得越来越小,所以我们并不需要担心 在接近极值点时,移动步伐过大而导致 错过极值点。
在迭代开始前,假设自变量 恰好初始化在函数的极小值或非常接近极小值的位置,会发生什么情况呢?
答:函数在极小值位置的导数 ,所以如果自变量 恰好位于这个位置,那么计算出的一小步为 ,因此 移动的距离就是 ,也就是 不会移动。如果 在非常接近极小值的位置,那么这个位置的导数 ,那么计算出的一小步为 ,因此 移动的距离微乎其微。所以,即使 已经位于极小值或非常接近极小值的位置,我们也不必担心 会远离这个位置。
建议
无论自变量 的初始位置在哪里,都不会影响最终的迭代结果,随着梯度下降算法的进行,都可以收敛到局部最优解。
