剑眉星目

深浅模式

递归、匿名、高阶、解耦 ​

更新: 2025/2/24 字数: 0 字 时长: 0 分钟

递归函数 ​

递归函数（recursion function）就是函数通过直接或间接的方式调用自身的函数。它主要包含“递”、“归”两个阶段：

  1. 递：在程序层面，函数不断深入地调用自身，通常传入更小或更简化的参数，直到达到“终止条件”。在系统层面，当函数被调用时，系统会在“调用栈”上为该函数分配新的栈帧，用于存储函数的局部变量、参数、返回地址等数据。
  2. 归：在程序层面，触发“终止条件”后，程序从最深层的递归函数开始逐层返回，汇聚每一层的结果。在系统层面，当函数完成执行并返回时，对应的栈帧会被从“调用栈”上移除，恢复之前函数的执行环境。

而从实现的角度看，递归代码主要包含三个要素：

  1. 终止条件：用于决定什么时候由“递”转“归”。
  2. 递归调用：对应“递”，函数调用自身，通常输入更小或更简化的参数。
  3. 返回结果：对应“归”，将当前递归层级的结果返回至上一层。

递归使用 ​

观察以下代码，我们只需调用函数 recur(n) ，就可以完成 1+2+⋯+n1+2+{\cdots}+n​ 的计算：

python
def recur(n: int) -> int:
    """递归"""
    # 终止条件
    if n == 1:
        return 1
    # 递：调用自身
    res = recur(n - 1)
    # 归：返回结果
    return n + res

求和函数的递归过程

虽然从计算角度看，循环与递归都可以得到相同的结果，但它们代表了两种完全不同的思考和解决问题的范式。

  • 循环：“自下而上”地解决问题。从最基础的步骤开始，然后不断重复或累加这些步骤，直到任务完成。
  • 递归：“自上而下”地解决问题。将原问题分解为更小的子问题，这些子问题和原问题具有相同的形式。接下来将子问题继续分解为更小的子问题，直到基本情况时停止（基本情况的解是已知的）。

以上述求和函数为例，设问题 f(n)=1+2+⋯+nf(n)=1+2+{\cdots}+n 。

  • 循环：在循环中模拟求和过程，从 11 遍历到 nn ，每轮执行求和操作，即可求得 f(n)f(n) 。
  • 递归：将问题分解为子问题 f(n)=n+f(n−1)f(n)=n+f(n-1) ，不断（递归地）分解下去，直至基本情况 f(1)=1f(1)=1 时终止。

递归原理 ​

递归函数每次调用自身时，系统都会为新开启的函数分配内存，以存储局部变量、调用地址和其他信息等，这将导致以下两方面的结果：

  • 耗内存：函数的上下文数据都存储在称为“栈帧空间”的内存区域中，直至函数返回后才会被释放。因此，递归通常比循环更加耗费内存空间。
  • 低效率：递归调用函数会产生额外的开销。因此，递归通常比循环的时间效率更低。

在触发终止条件前，同时存在 nn 个未返回的递归函数，递归深度为 nn 。

递归调用深度

递归错误 ​

在 Python 中允许的递归深度通常是有限的，过深的递归可能导致栈溢出错误。例如，我们写一个了递归函数如下：

python
def foo():   # 注释：声明foo函数。
    print('hello')
    main()   # 注释：又返回调用main函数。

def main():  # 注释：声明main函数。
    foo()

if __name__ == '__main__':
    main()   # 注释：输出多个'hello'后，超过最大递归深度，出现递归错误。

上面递归函数中出现错误的原因是：函数在调用的时候会将函数放到调用栈中，而递归函数在不断的调用自身，也就是说无休止的往调用栈中添加函数，但调用栈的空间是有限的，当空间被耗光时，就会出现“超过最大递归深度”的错误。

QQ截图20230404173743

建议

官方 CPython 调用栈的大小默认是 1000 层，超过就报错。虽然我们可以通过 sys.setecursionlimit() 方法来修改调用栈的大小，但最好不要擅自修改。

递归注意 ​

明白了“函数调用”的原理以及“递归错误”产生的原因，以后在使用递归函数时要注意以下几点：

  1. 写递归函数一定要找到递归公式，也就是第 nn 次和第 n−1n-1 次的关系。
  2. 不管是调用别的函数，还是调用自身函数，一定要做到快速收敛，即在有限的调用次数内通过收敛条件来结束掉函数，而不是无限制的调用函数，否则出现 RecursionError: maximum recursion depth exceeded... 超过最大递归深度递的错误。
  3. 递归函数效率低下，因为每一次调用函数，都需要先保存现场，调用完后还要恢复现场，而且调用栈也要为其分配空间。因此循环能做的事情，虽然递归函数也可以做，尽量不使用递归。
  4. 如果非要使用递归，我们可以通过两种方法来加速函数运算：1、增加字典保存结果；2、使用 functools 模块中的 lru_cache 装饰器函数来缓存最近的结果。

斐波那契数 ​

斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：0,1,1,2,3,5,8,13,⋯0,1,1,2,3,5,8,13,{\cdots} ，求该数列的第 nn 个数字，那么设斐波那契数列的第 nn 个数字为 f(n)f(n) ，易得两个结论：

  • 数列的前两个数字为 f(1)=0f(1)=0 和 f(2)=1f(2)=1 。
  • 数列中的每个数字是前两个数字的和，即 f(n)=f(n−1)+f(n−2)f(n)=f(n-1)+f(n-2) 。

按照递推关系进行递归调用，将前两个数字作为终止条件，便可写出递归代码。调用 fib(n) 即可得到斐波那契数列的第 nn 个数字：

python
"""
斐波那契数列：递归
"""
def fib(n: int) -> int:
    # 终止条件
    if n == 1 or n == 2:
        return n - 1
    # 递归调用
    return fib(n - 1) + fib(n - 2)

观察以上代码，我们在函数内递归调用了两个函数，这意味着从一个调用产生了两个调用分支。如下图所示，这样不断递归调用下去，最终将产生一棵层数为 nn 的递归树（recursion tree）。

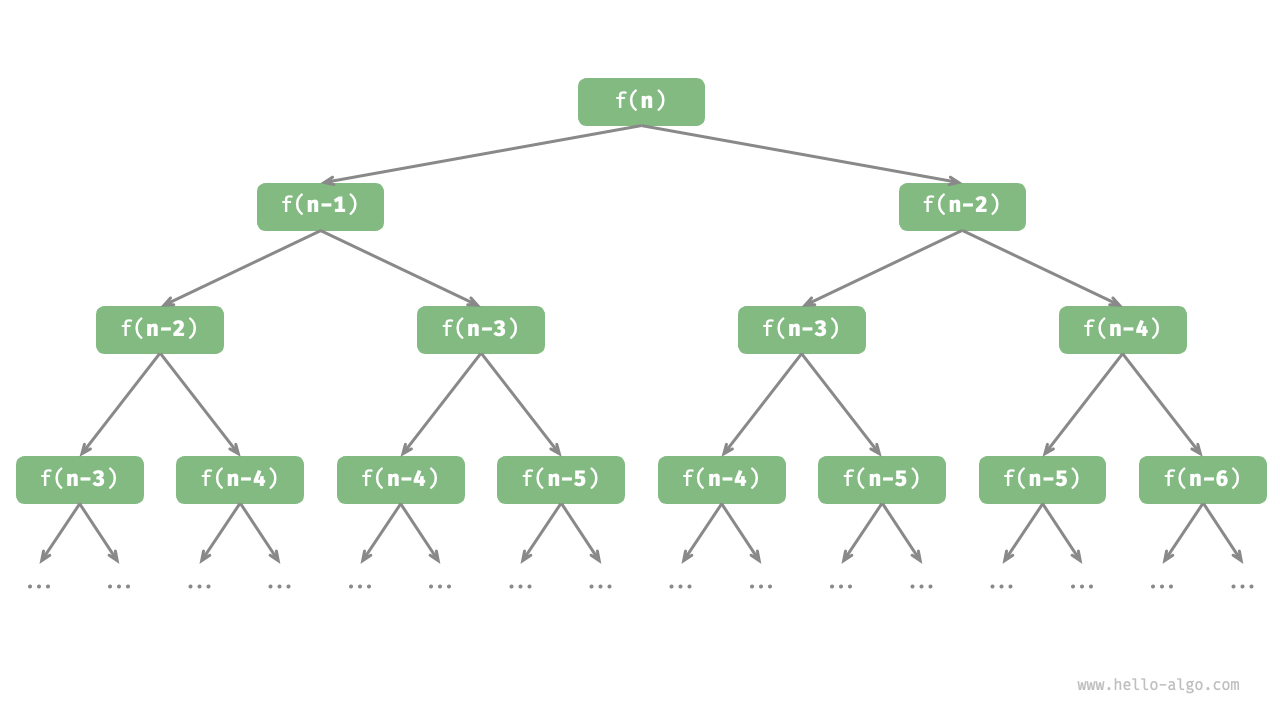
斐波那契数列的递归树

从本质上看，递归体现了“将问题分解为更小子问题”的思维范式，这种分治策略至关重要：

  • 从算法角度看，搜索、排序、回溯、分治、动态规划等许多重要算法策略直接或间接地应用了这种思维方式。
  • 从数据结构角度看，递归天然适合处理链表、树和图的相关问题，因为它们非常适合用分治思想进行分析。

不过当我们在电脑上运行递归函数时，会看到耗时很长。这是因为使用的函数每次的返回值等于前两个函数的返回值之和（递归函数），因此每向后计算一个斐波拉切数所消耗的时间约等于计算上一个斐波拉切数所消耗时间的两倍。这时可以理解到在递归函数中其实有大量的重复运算，我们只需要增加一些空间（例如使用字典）来记住上一次的运算结果，就可以快速算出答案。代码如下：

python
# 优化（增加temp字典保存中间结果）
def fib(num=40, temp={}):
    if num in (1, 2):
        return 1
    if num not in temp:
        temp[num] = fib(num - 1) + fib(num - 2)
    return temp[num]

除了使用字典，我们还可以使用变量交换累加的方法来计算斐波拉切数，仅仅增加两个变量即可，这是一种更高效的算法：

python
def fib(num=40):
    a, b = 0, 1
    for _ in range(num):
        a, b = a + b, a
    return a

汉诺塔问题 ​

汉诺塔来源于一个印度传说，其情节就是：大梵天创造世界的时候做了三根石柱，在一根柱子上从下往上按照大小顺序叠着 64 片圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一个柱子上，而且小圆盘上不能放大圆盘，每次只能移动一个圆盘，64 片圆盘移动完毕之日，就是世界毁灭之时。

QQ截图20230527124142

我们首先缩小问题的规模进行如下思考：

  • 当时圆盘数量为 1 时情况：
    • A 柱圆盘 1 移动到 C 柱，移动次数为1。
  • 当时圆盘数量为 2 时情况：
    • A 柱圆盘 1 移动到 B 柱，移动次数为 1。
    • A 柱圆盘 2 移动到 C 柱，移动次数为 2。
    • B柱圆盘 1 移动到 C 柱，移动次数为 3。
  • 当时圆盘数量为 3 时情况：
    • A 柱圆盘 1 移动到 C 柱，移动次数为 1。
    • A 柱圆盘 2 移动到 B 柱，移动次数为 2。
    • C 柱圆盘 1 移动到 B 柱，移动次数为 3。
    • A 柱圆盘 3 移动到 C 柱，移动次数为 4。
    • B 柱圆盘 1 移动到 A 柱，移动次数为 5。
    • B 柱圆盘 2 移动到 C 柱，移动次数为 6。
    • A 柱圆盘 1 移动到 C 柱，移动次数为 7。
  • 当时圆盘数量为 n 时情况：
    • 把圆盘 1 至圆盘 n-1 从 A 柱经过 C 柱移动到 B 柱。
    • 把圆盘 n 从 A 柱移动到 C 柱。
    • 把圆盘 1 至圆盘 n-1 从 B 柱经过 A 柱移动到 C 柱。
python
def hannoi(n, a, b, c):
    if n > 0:
        hannoi(n - 1, a, c, b)
        print(f"moving from {a} to {c}")
        hannoi(n - 1, b, a, c)
# 移动3个圆盘步骤
hannoi(3, 'A', 'B', 'C')
'''
输出：
moving from A to C
moving from A to B
moving from C to B
moving from A to C
moving from B to A
moving from B to C
moving from A to C
'''

建议

通过规律我们可以发现一个规律：移动次数 = 2 ** 圆盘数 - 1。移动 64 个圆盘需要移动的次数就是：2 ** 64 - 1 = 18446744073709551615，假设婆罗门每秒搬一个盘子，则总共需要 5800 亿年！

汉诺塔问题 ​

在归并排序和构建二叉树中，我们都是将原问题分解为两个规模为原问题一半的子问题。然而对于汉诺塔问题，我们采用不同的分解策略。

给定三根柱子，记为 A、B 和 C 。起始状态下，柱子 A 上套着 nn 个圆盘，它们从上到下按照从小到大的顺序排列。我们的任务是要把这 𝑛 个圆盘移到柱子 C 上，并保持它们的原有顺序不变。在移动圆盘的过程中，需要遵守以下规则。

  1. 圆盘只能从一根柱子顶部拿出，从另一根柱子顶部放入。
  2. 每次只能移动一个圆盘。
  3. 小圆盘必须时刻位于大圆盘之上。

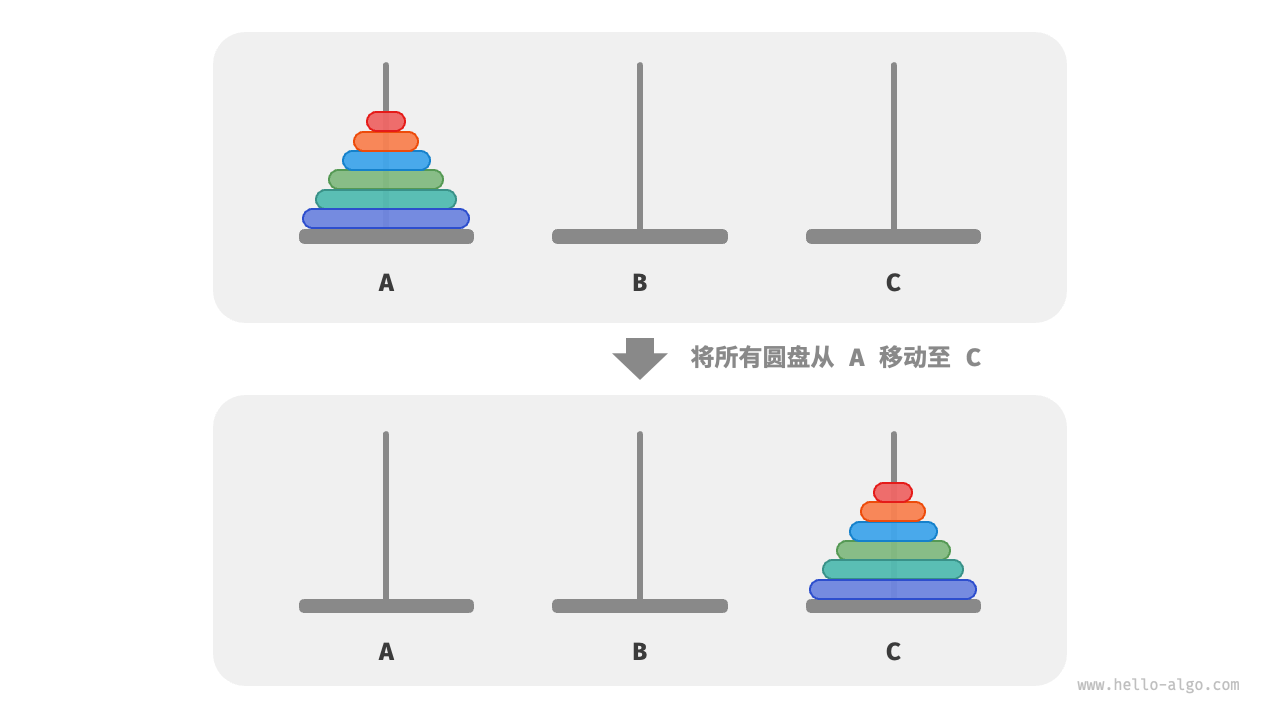
汉诺塔问题示例

我们将规模为 ii 的汉诺塔问题记作 f(i)f(i) 。例如 f(3)f(3) 代表将 33 个圆盘从 A 移动至 C 的汉诺塔问题。

基本情况 ​

如下图所示，对于问题 f(1)f(1) ，即当只有一个圆盘时，我们将它直接从 A 移动至 C 即可。

::: image-group

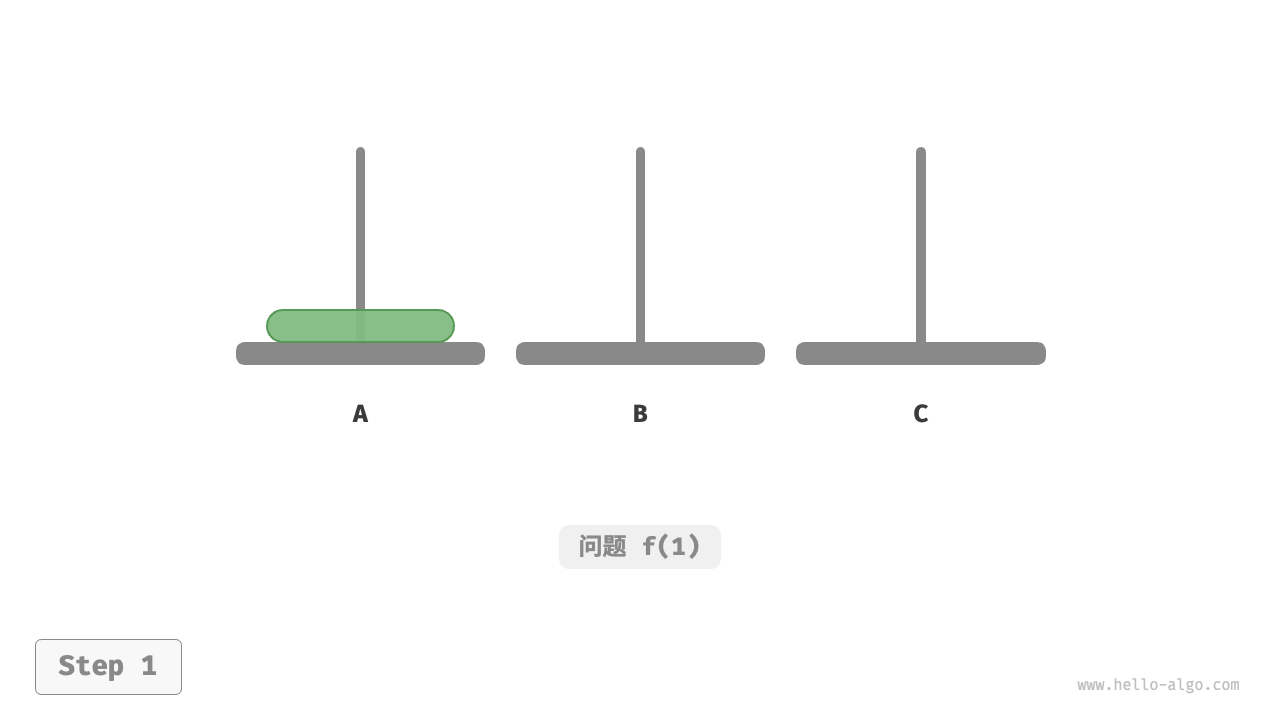
Step 1

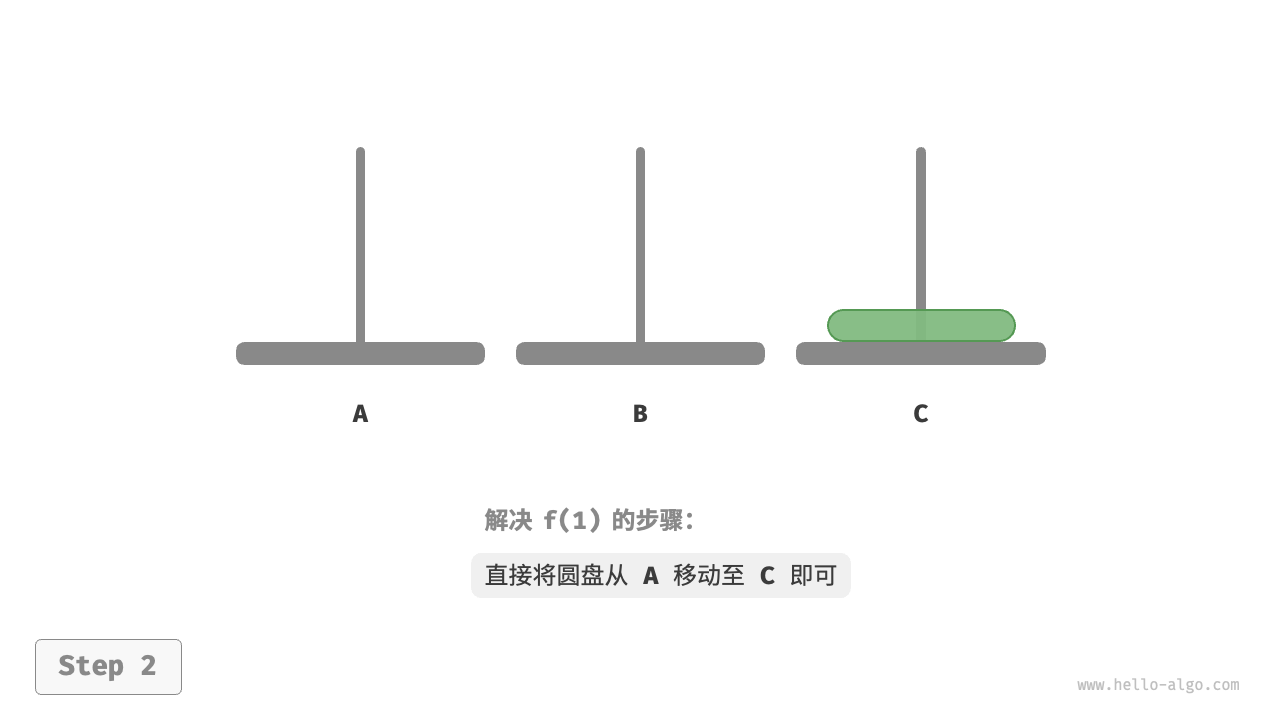
Step 2

:::

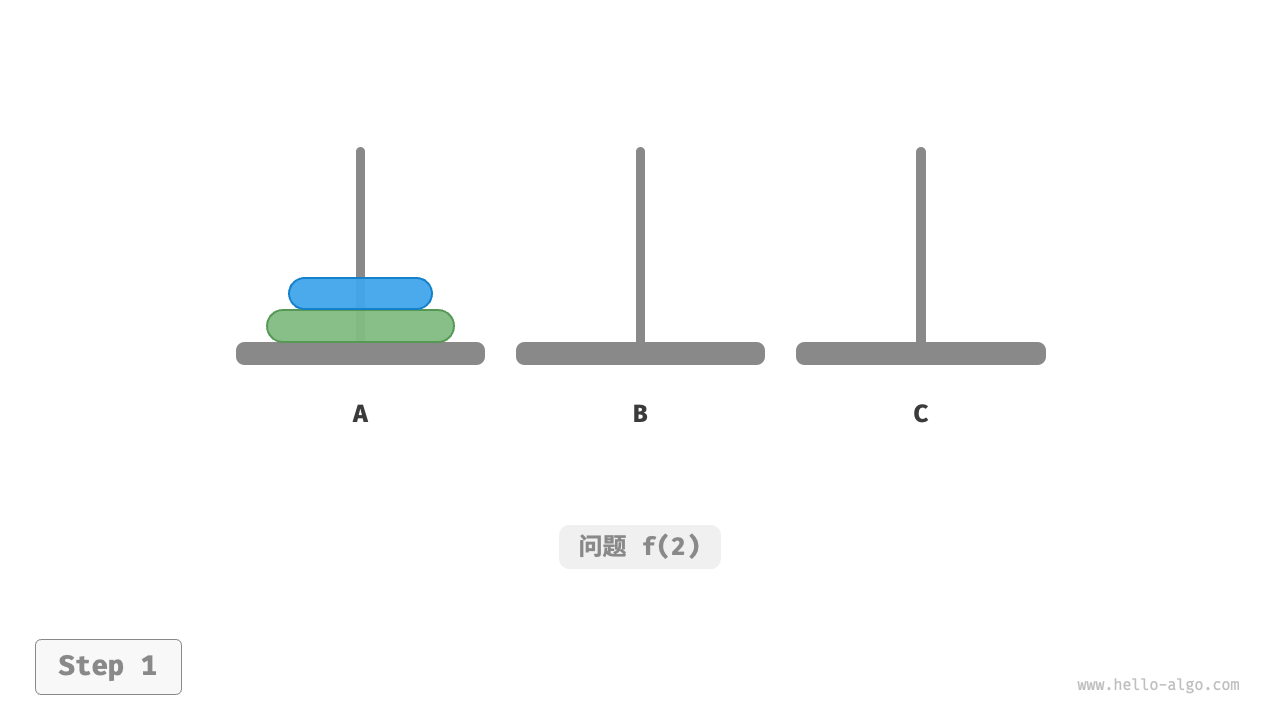
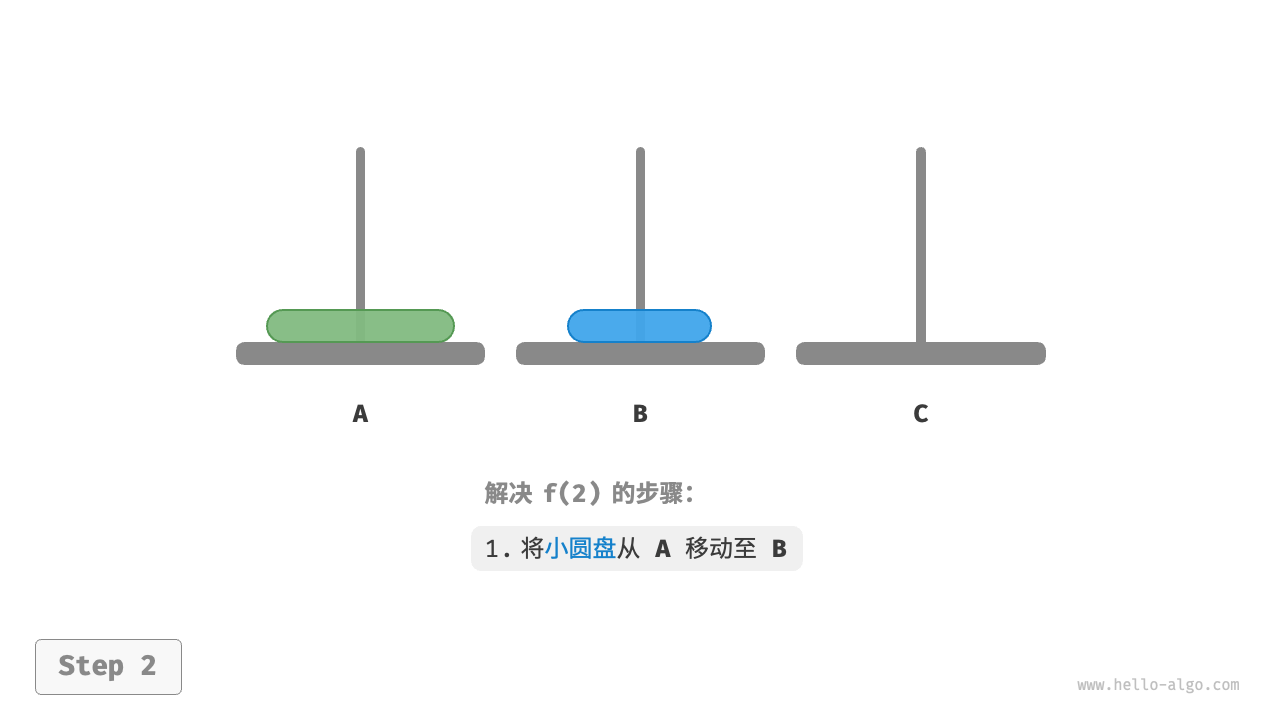
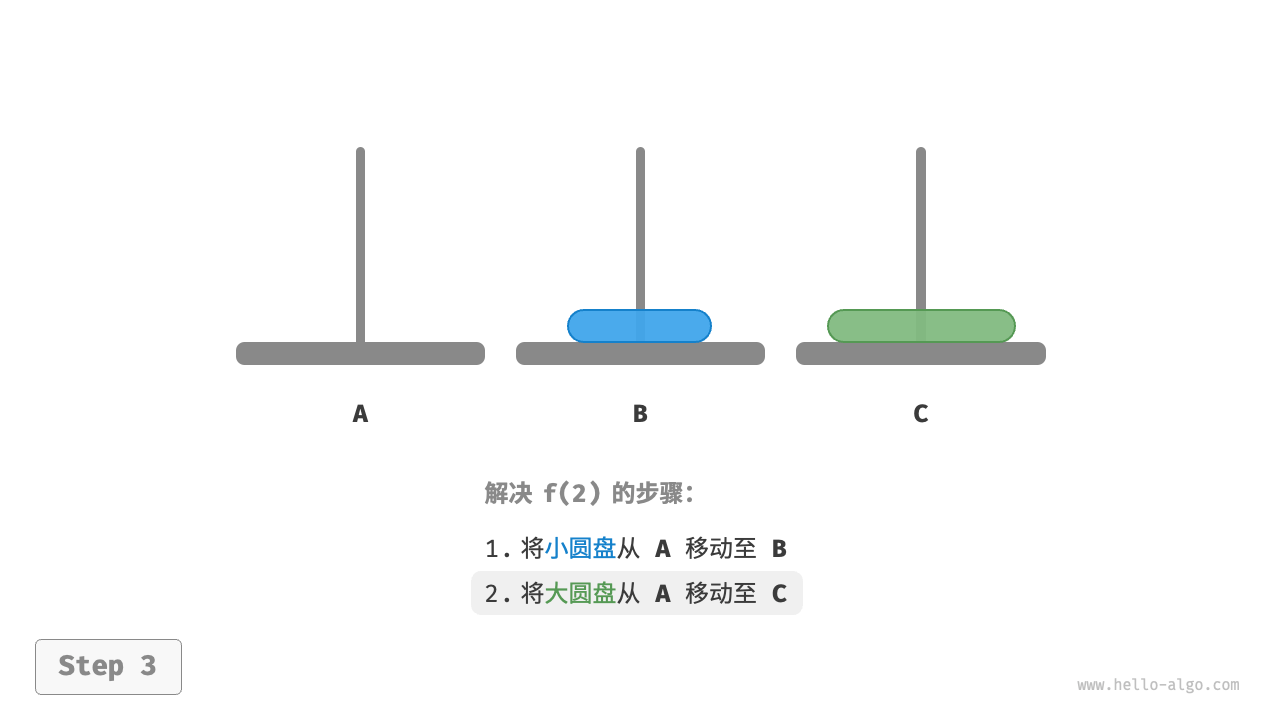
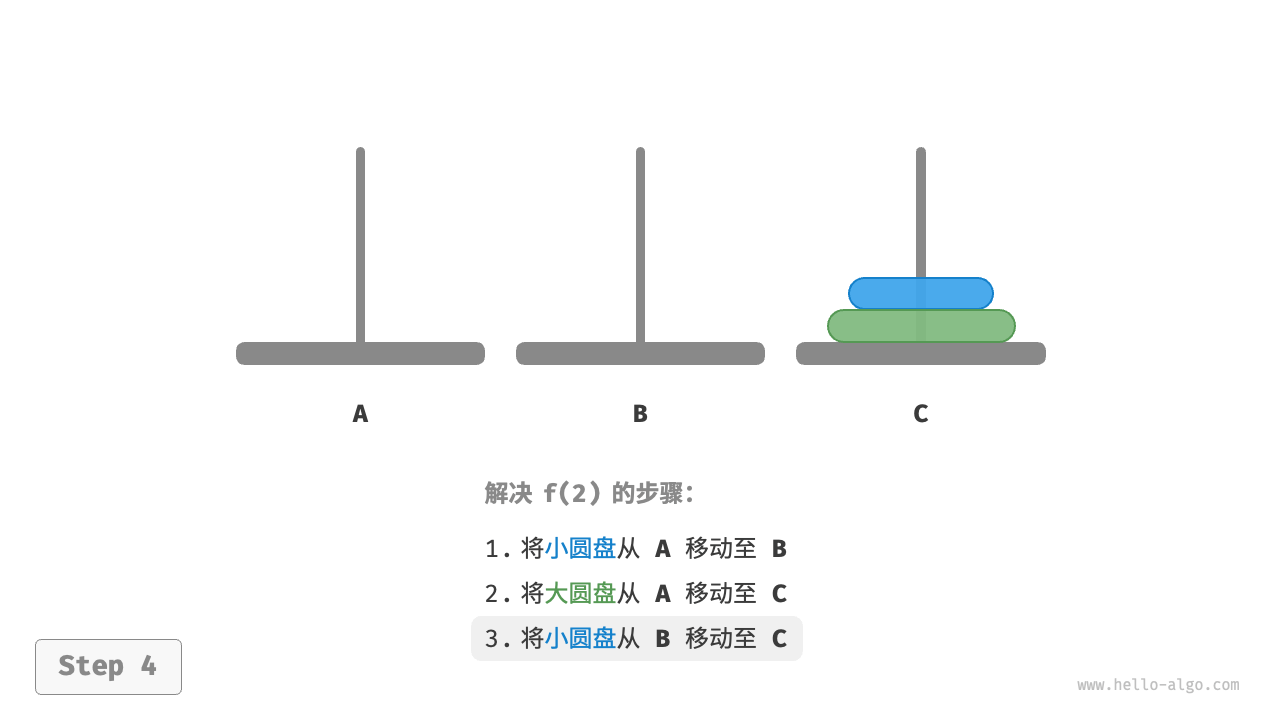
如下图所示，对于问题 f(2)f(2) ，即当有两个圆盘时，由于要时刻满足小圆盘在大圆盘之上，因此需要借助 B 来完成移动。

  1. 先将上面的小圆盘从 A 移至 B 。
  2. 再将大圆盘从 A 移至 C 。
  3. 最后将小圆盘从 B 移至 C 。

::: image-group

Step 1

Step 2

Step 3

Step 4

:::

解决问题 f(2)f(2) 的过程可总结为：将两个圆盘借助 B 从 A 移至 C 。其中，C 称为目标柱、B 称为缓冲柱。

子问题分解 ​

对于问题 f(3)f(3) ，即当有三个圆盘时，情况变得稍微复杂了一些。

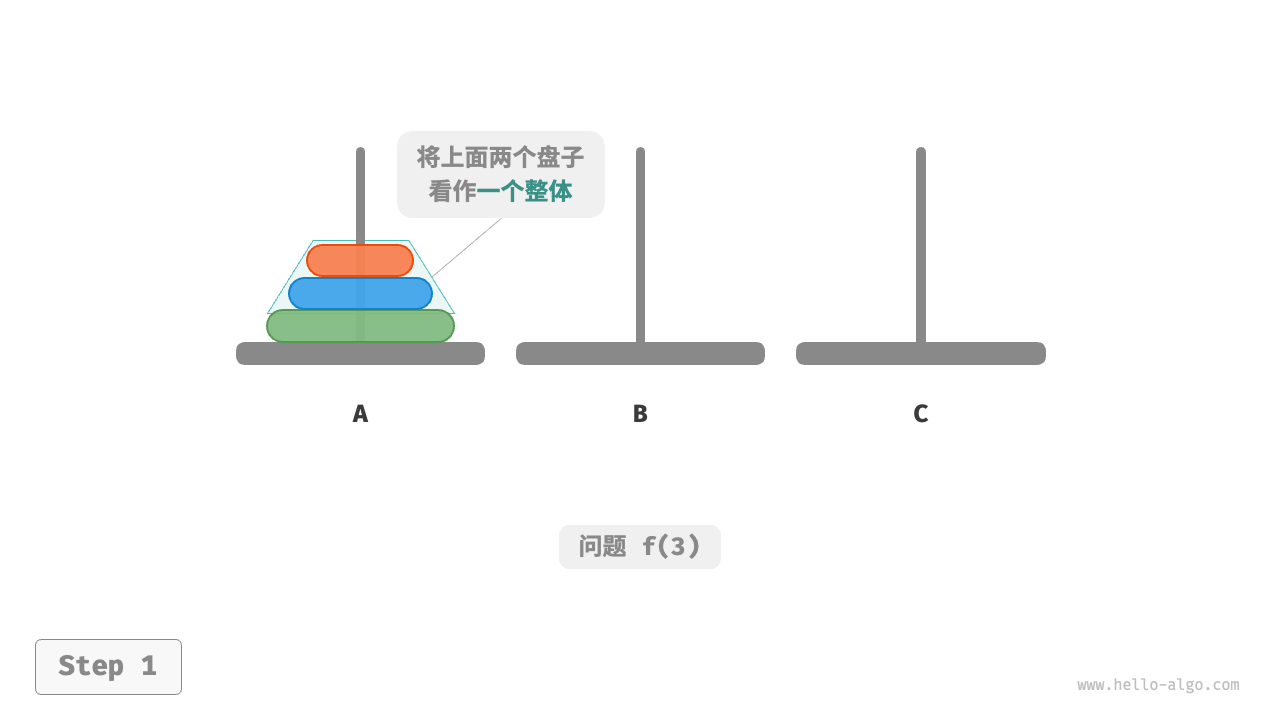
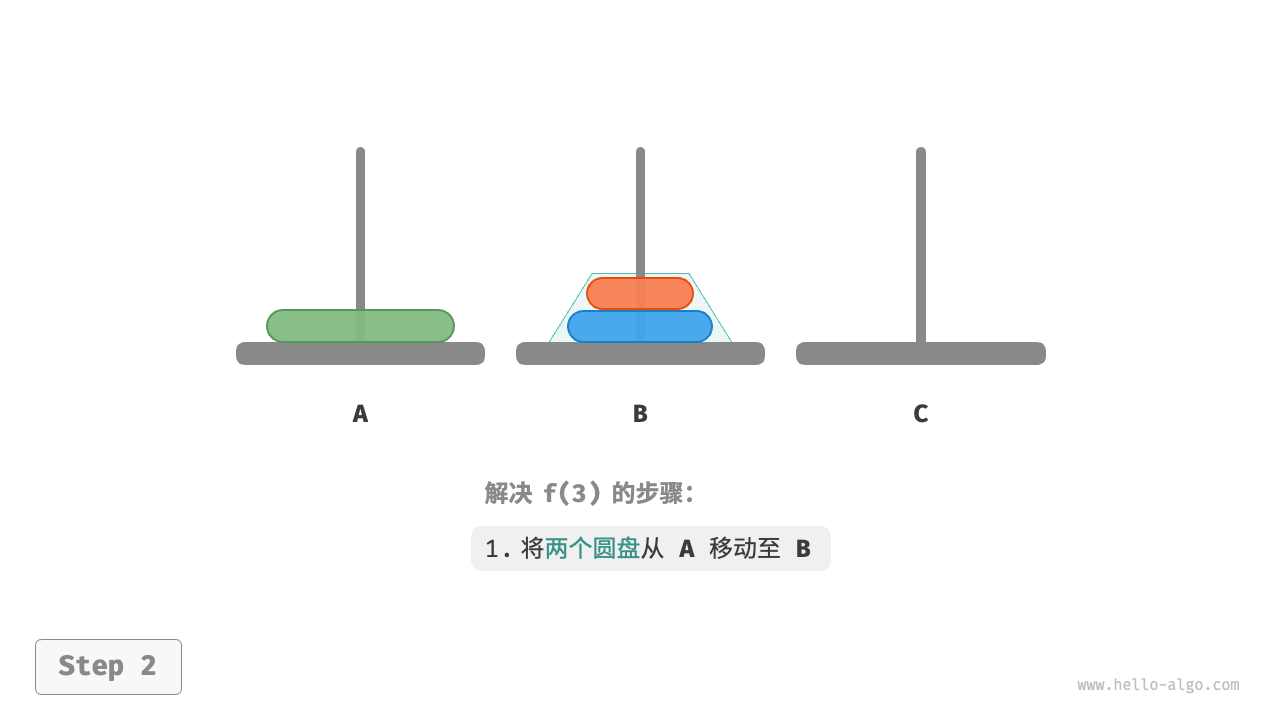
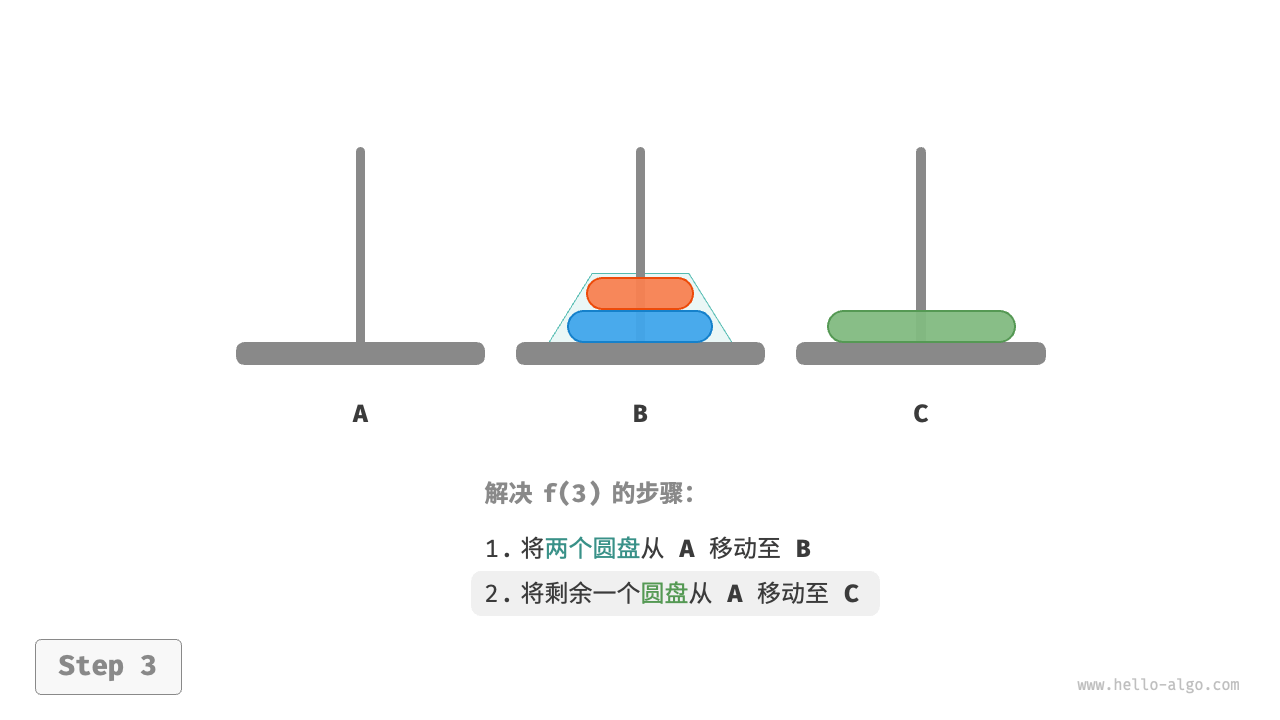
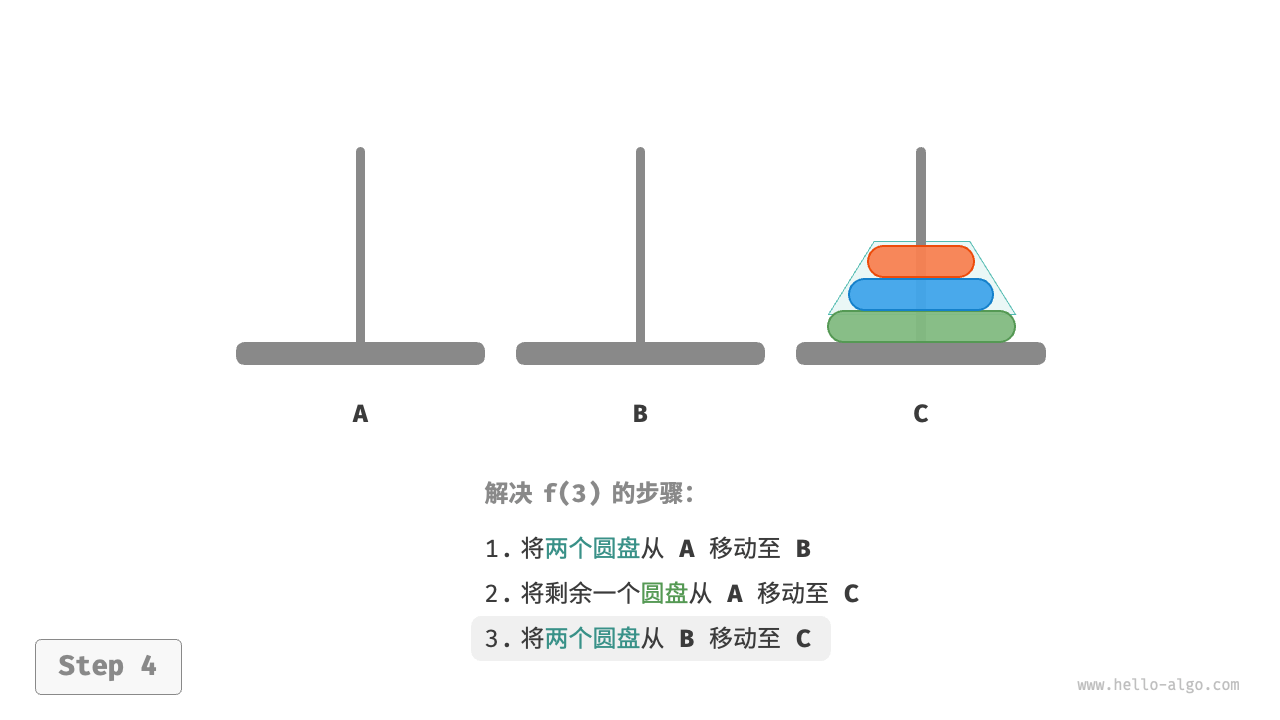
因为已知 f(1)f(1) 和 f(2)f(2) 的解，所以我们可从分治角度思考，将 A 顶部的两个圆盘看作一个整体，执行下图所示的步骤。这样三个圆盘就被顺利地从 A 移至 C 了。

  1. 令 B 为目标柱、C 为缓冲柱，将两个圆盘从 A 移至 B 。
  2. 将 A 中剩余的一个圆盘从 A 直接移动至 C 。
  3. 令 C 为目标柱、A 为缓冲柱，将两个圆盘从 B 移至 C 。

::: image-group

Step 1

Step 2

Step 3

Step 4

:::

从本质上看，我们将问题 f(3)f(3) 划分为两个子问题 f(2)f(2) 和一个子问题 f(1)f(1) 。按顺序解决这三个子问题之后，原问题随之得到解决。这说明子问题是独立的，而且解可以合并。

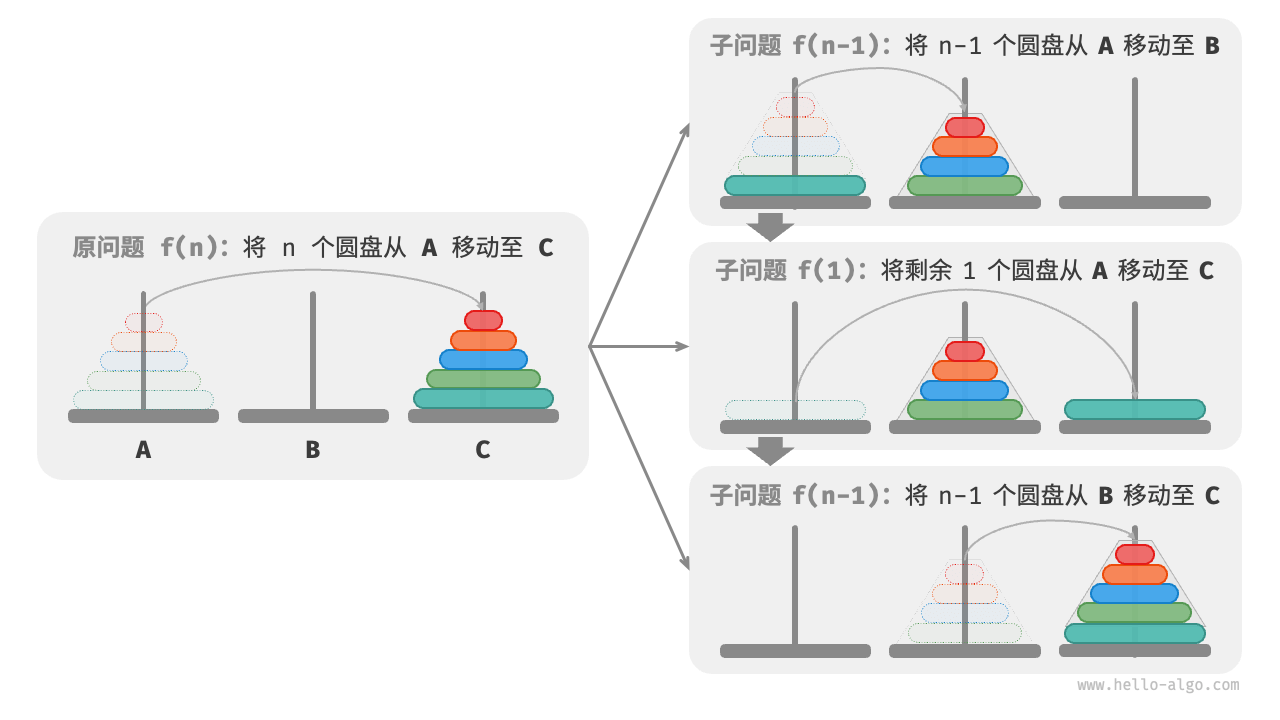
至此，我们可总结出下图所示的解决汉诺塔问题的分治策略：将原问题 f(n)f(n) 划分为两个子问题 f(n−1)f(n-1) 和一个子问题 f(1)f(1) ，并按照以下顺序解决这三个子问题。

  1. 将 n−1n-1 个圆盘借助 C 从 A 移至 B 。
  2. 将剩余 11 个圆盘从 A 直接移至 C 。
  3. 将 n−1n-1 个圆盘借助 A 从 B 移至 C 。

对于这两个子问题 f(n−1)f(n-1) ，可以通过相同的方式进行递归划分，直至达到最小子问题 f(1)f(1) 。而 f(1)f(1) 的解是已知的，只需一次移动操作即可。

解决汉诺塔问题的分治策略

代码实现 ​

在代码中，我们声明一个递归函数 dfs(i, src, buf, tar) ，它的作用是将柱 src 顶部的 𝑖 个圆盘借助缓冲柱 buf 移动至目标柱 tar ：

python
def move(src: list[int], tar: list[int]):
    """移动一个圆盘"""
    # 从 src 顶部拿出一个圆盘
    pan = src.pop()
    # 将圆盘放入 tar 顶部
    tar.append(pan)

def dfs(i: int, src: list[int], buf: list[int], tar: list[int]):
    """求解汉诺塔问题 f(i)"""
    # 若 src 只剩下一个圆盘，则直接将其移到 tar
    if i == 1:
        move(src, tar)
        return
    # 子问题 f(i-1) ：将 src 顶部 i-1 个圆盘借助 tar 移到 buf
    dfs(i - 1, src, tar, buf)
    # 子问题 f(1) ：将 src 剩余一个圆盘移到 tar
    move(src, tar)
    # 子问题 f(i-1) ：将 buf 顶部 i-1 个圆盘借助 src 移到 tar
    dfs(i - 1, buf, src, tar)

def solve_hanota(A: list[int], B: list[int], C: list[int]):
    """求解汉诺塔问题"""
    n = len(A)
    # 将 A 顶部 n 个圆盘借助 B 移到 C
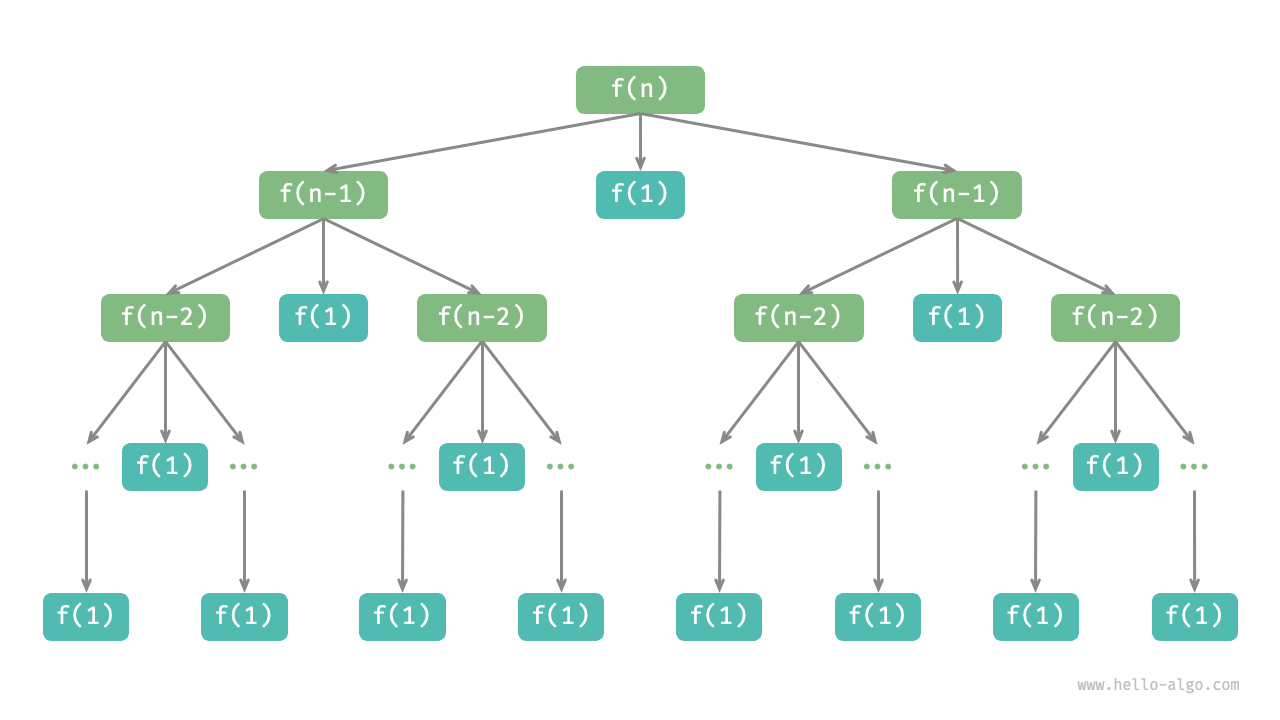
    dfs(n, A, B, C)

如下图所示，汉诺塔问题形成一棵高度为 nn 的递归树，每个节点代表一个子问题，对应一个开启的 dfs() 函数，因此时间复杂度为 O(2n)O(2^n) ，空间复杂度为 O(n)O(n) 。

汉诺塔问题的递归树

提醒

汉诺塔问题源自一个古老的传说。在古印度的一个寺庙里，僧侣们有三根高大的钻石柱子，以及 6464 个大小不一的金圆盘。僧侣们不断地移动圆盘，他们相信在最后一个圆盘被正确放置的那一刻，这个世界就会结束。

然而，即使僧侣们每秒钟移动一次，总共需要大约 264≈1.84×10192^{64}\approx1.84\times10^{19} 秒，合约 58505850 亿年，远远超过了现在对宇宙年龄的估计。所以，倘若这个传说是真的，我们应该不需要担心世界末日的到来。

算数的阶乘 ​

阶乘的定义：n!=n×(n−1)×(n−2)⋯×2×1n!=n{\times}(n-1){\times}(n-2){\cdots}{\times}2{\times}1

  • 使用递归的方式求阶乘，代码如下：
python
# 使用递归的方式求阶乘
def fac_1(num):
    if num == 1:    # 注释：收敛条件。
        return 1
    return num * fac_1(num - 1)
print(fac_1(10))    # 输出：3628800
print(fac_1(1000))  # 报错：超出最大递归深度。注释：循环能做的事情，尽量不使用递归。
  • 使用循环的方式求阶乘，代码如下：
python
def fac_2(num):
    result = 1
    for i in range(2, num + 1):
        result *= i
    return result
print(fac_2(10))    # 输出：3628800
print(fac_2(1000))  # 输出：4023872...

爬楼梯方案 ​

爬楼梯 - nn 个台阶，一次可以爬 11 个、22 个、33 个，爬完 nn 个台阶一共有多少种走法？（提示：第 nn 个台阶的走法等于 n−1n-1、n−2n-2、n−3n-3 个台阶的走法之和。）

  • 使用递归的方式求走法之和，代码如下：
python
def climb_1(num):
    if num == 0:
        return 1
    elif num < 0:
        return 0
    return climb_1(num - 1) + climb_1(num - 2) + climb_1(num - 3)
print(climb_1(10))    # 输出：274
print(climb_1(1000))  # 报错：超出最大递归深度。注释：循环能做的事情，尽量不使用递归。
  • 使用循环的方式求走法之和，代码如下：
python
def climb_2(num):
    a, b, c = 2, 1, 1
    for i in range(num):
        a, b, c = a + b + c, a, b
    return c
print(climb_2(10))    # 输出：274
print(climb_2(1000))  # 输出：275884...

提醒

以上述递归函数为例，求和操作在递归的“归”阶段进行。这意味着最初被调用的函数实际上是最后完成其求和操作的，这种工作机制与栈的“先入后出”原则异曲同工。事实上，“调用栈”和“栈帧空间”这类递归术语已经暗示了递归与栈之间的密切关系。

与迭代对比 ​

总结以上内容，迭代和递归在实现、性能和适用性上有所不同：

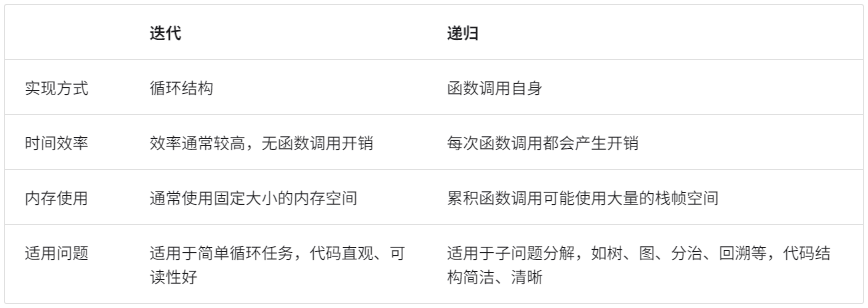
image-20240511141026623

总之，选择迭代还是递归取决于特定问题的性质。在编程实践中，权衡两者的优劣并根据情境选择合适的方法至关重要。

匿名函数 ​

匿名函数：以一种简单的方式来构建功能简单的函数。

使用格式：函数名 = lambda 形参: 返回值表达式

python
# 普通函数
def my_sum(x, y):
    return x + y, x * y

print(my_sum(10, 20))                   # 输出：(30, 200)

# 包含加法和乘法的匿名函数
lam_sum = lambda x, y: (x + y, x * y)
print(lam_sum(10, 20))                  # 输出：(30, 200)

# 包含逻辑和判断的匿名函数
lam_fun = lambda i: i % 2 == 0 and i > 3
print([lam_fun(i) for i in [3, 4, 5]])  # 输出：[False, True, False]

映射函数 ​

在很多时候，我们会遇到将一个可迭代对象通过映射关系输出为对应值的情况，这时我们可能会选择 for 循环来处理：

python
a = {'1': '法人', '2': '高管', '3': '负责人'}
b = ['1', '3']
c = '13'
print(list(a.get(i) for i in b))  # 输出：['法人', '负责人']
print(list(a.get(i) for i in c))  # 输出：['法人', '负责人']

其实上，在 Python 中有专门处理映射关系的 map(函数名, 可迭代对象) 内置函数，它可以将可迭代对象中的每个元素都通统一经过指定函数进行处理，返回一个 map 对象，再用 list() 函数转换为列表。需要注意的是，在使用的过程中不论是函数或内置的方法都不要带括号，也不需要遍历传参，它会自己处理。

python
a = {'1': '法人', '2': '高管', '3': '负责人'}
b = ['1', '3']
c = '13'
print(list(map(a.get, b)))  # 输出：['法人', '负责人']
print(list(map(a.get, c)))  # 输出：['法人', '负责人']

同样的我们也可以使用 map 映射函数来批量处理数据：这里也一样，str 类型内置的 upper 方法不要带括号，也不需要遍历传参，它会自己处理。

python
w = ['apple', 'banana', 'cherry']
print(list(map(str.upper, w)))  # 输出：['APPLE', 'BANANA', 'CHERRY']

如果需要自定义函数进行处理的话，我们可以这样来写：这里也一样，自定义的函数也不要带括号，也不需要遍历传参，它会自己处理。

python
# 统一变换函数
def convert_int(item):
    return int(item)

print(list(map(convert_int, '6688')))  # 输出：[6, 6, 8, 8]。注释：将map对象转化为列表list。
print(list(map(int, '6688')))          # 输出：[6, 6, 8, 8]。注释：直接使用内置的int函数来转换可迭代对象中的每一个元素。

如果需要匿名函数进行处理的话，我们可以这样来写：这里也一样，匿名函数也不要带括号，也不需要遍历传参，它会自己处理。

python
# 包含逻辑和判断的匿名函数
lam_fun = lambda i: i % 2 == 0 and i > 3
print(list(map(lam_fun, [3, 4, 5])))  # 输出：[False, True, False]

高阶函数 ​

前面我们所学所写的函数都是“一阶函数”，而把函数作为函数的参数或返回值的这种方式通常称之为“高阶函数”。

python
# 高阶函数
def add_num(fun, x, y):      # 注释：高阶函数add_num的形参fun接收实参sum求和函数。
    return fun([x, y])

print(add_num(sum, 10, 20))  # 输出：30

高阶函数常用于降低函数的耦合度（解耦），所谓的“藕合度”指程序模块间存联系紧密程度 ，模块间关联少越独立，其耦合度就越低；而“内聚性”则是指模块内部相互依赖程度，所干事情少功能越单一，内聚性就越高。通常我们在设计函数的时候，最好要做到“高内聚低耦合”，因为在软件设计中通常用耦合度和内聚度作为衡量模块独立程度的标准。

  • 高内聚：每个成员方法只完成一件事（最大限度的聚合）。
  • 低耦合：减少一个成员方法内部调用另一个成员方法。

高耦合 ​

这里我们写两个计算加法和乘法的函数，代码如下：这里可以看到，下面两个方法的代码几乎是一模一样，而造成代码的重复原因是因为函数和运算方法耦合在了一起，导致代码缺乏灵活性。

python
# 计算加法函数
def add(*args, **kwargs):
    total = 0
    for arg in args:
        if type(arg) in (int, float):
            total += arg
    for value in kwargs.values():
        if type(value) in (int, float):
            total += value
    return total

# 计算乘法函数
def mul(*args, **kwargs):
    total = 1
    for arg in args:
        if type(arg) in (int, float):
            total *= arg
    for value in kwargs.values():
        if type(value) in (int, float):
            total *= value
    return total

print(add(11, 22, 33, 44))  # 输出：110
print(mul(11, 22, 33, 44))  # 输出：351384

提醒

代码有很多种坏味道，而重复是最坏的一种。

低耦合 ​

降低耦合的方法也很简单，就是给函数再加参数，把写死的代码变成灵活的参数传进去。这里的加法运算函数、乘法运算函数也可以变成函数的参数直接传进来，代码如下：

python
# 加法运算函数
def add(x, y):
    return x + y

# 乘法运算函数
def mul(x, y):
    return x * y

# 通用运算函数，init_value初始值，fn二元运算函数
def calc(init_value, fn, *args, **kwargs):
    total = init_value
    for arg in args:
        if type(arg) in (int, float):
            total = fn(total, arg)
    for value in kwargs.values():
        if type(value) in (int, float):
            total = fn(total, value)
    return total

print(calc(0, add, 11, 22, 33, 44))  # 输出：110
print(calc(1, mul, 11, 22, 33, 44))  # 输出：351384

可以看到，通用运算函数形参 fn 接收的参数是函数对象，因此通用运算函数是一个高阶函数，而且通用运算函数既可以实现加法运算，也可以实现乘法运算，这是因为通用运算函数并没有和加法运算、乘法运算耦合在一起，因此这个函数的通用性、灵活性是远远高于前面一个版本的函数。同时也说明，使用高阶函数可以实现对原有函数的解耦合操作。这时有人会说，上面还不是写了加法运算函数、乘法运算函数。如果不想写，可以使用 operator 模块里面封装的各种二元运算函数，代码如下：

python
# add加法运算函数、mul乘法运算函数
from operator import add, mul

# 通用运算函数，init_value初始值，fn二元运算函数
def calc(init_value, fn, *args, **kwargs):
    total = init_value
    for arg in args:
        if type(arg) in (int, float):
            total = fn(total, arg)
    for value in kwargs.values():
        if type(value) in (int, float):
            total = fn(total, value)
    return total

print(calc(0, add, 11, 22, 33, 44))  # 输出：110
print(calc(1, mul, 11, 22, 33, 44))  # 输出：351384

如果不想使用 operator 模块，我们还可以添加匿名函数 lambda 实现解耦合操作：

python
# 通用运算函数，init_value初始值，fn二元运算函数
def calc(init_value, fn, *args, **kwargs):
    total = init_value
    for arg in args:
        if type(arg) in (int, float):
            total = fn(total, arg)
    for value in kwargs.values():
        if type(value) in (int, float):
            total = fn(total, value)
    return total

# lambda加法运算
print(calc(0, lambda x, y : x + y, 11, 22, 33, 44))  # 输出：110
# lambda乘法运算
print(calc(1, lambda x, y : x * y, 11, 22, 33, 44))  # 输出：351384