求导计算

更新: 2025/2/24 字数: 0 字 时长: 0 分钟

本节我们会讲解如何使用 PyTorch，自动计算函数关于自变量的偏导数。

自动微分

对于一元函数 $f(x)=x^2+3x+2$，我们可以手动求出 $f$ 关于 $x$ 的导数，结果是：

$f'(x)=2x+3$

对于二元函数 $f(x,y)=x^2+y^2$，我们同样可以手动求出 $f$ 关于 $x$ 和 $y$ 的偏导数，结果是：

$\begin{aligned} \frac{\partial f}{\partial x}=2x\\ \frac{\partial f}{\partial y}=2y\\ \end{aligned}$

随着函数变得更加复杂，手动推导也会变得非常复杂起来，例如下面这个函数 $f$：

$f(a,b,c,d,e)=\frac{a^3b^2}{ln(c+1)}+e^{ad}\cos(bc)+\sqrt{a^2+b^2}\cdot\ln(d^2+e^2)$

可以看到这个函数自变量更多，要手动求函数 $f$ 关于 $a$、$b$、$c$、$d$、$e$ 的偏导数就会非常复杂，这就需要使用 PyTorch 的自动微分了。PyTorch 的自动微分是一种自动计算导数和梯度的技术，无论函数多么复杂，都可以帮助我们自动实现梯度的计算。另外，自动微分的内部还会通过链式法则，跟踪推导目标函数 $L$ 关于权重 $w$ 的梯度。

样例代码

基于自动微分，我们不再需要一步步的推导计算，从而可以更容易地实现梯度下降算法。

手动计算

这里可以先来看手动计算一元函数 $f(x)=x^2+3x+2$ 梯度，具体代码如下：运行代码，可以看到蓝色的抛物线对应函数 $f(x)$，橙色的直线对应导函数 $f'(x)$ 。

import numpy as np
import matplotlib.pyplot as plt

# 定义二次函数f(x) = x ^ 2 + 3 * x + 2
def f(x):  
    return x * x + 3 * x + 2

# 手动推导出函数f(x)的导数df(x) = 2 * x + 3
def df(x): 
    return 2 * x + 3

if __name__ == '__main__':
    # 生成1000个范围在(-6.5, 3.5)之间的自变量x的序列
    x = np.linspace(-6.5, 3.5, 1000)
    y_f = f(x) # 计算函数值
    y_df = df(x) # 计算导函数值
    # 绘制f和df的图像
    plt.plot(x, y_f, label='f(x) = x * x + 3 * x + 2')
    plt.plot(x, y_df, label="f'(x) = 2 * x + 3")
    plt.legend()
    plt.grid(True)
    plt.show()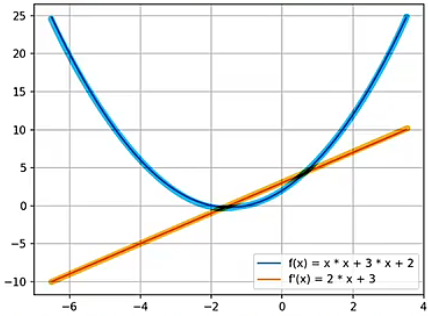

自动计算

使用 PyTorch 的自动微分功能，我们就只需要定义原函数 $f(x)$ 即可，然后通过 backward 函数自动计算梯度，就不再需要定义导函数 $df(x)$ 了，具体代码如下：运行代码，可以看到和上面面相同的图案。

import torch
import matplotlib.pyplot as plt

# 定义原函数f(x)
def f(x):
    return x * x + 3 * x + 2

if __name__ == '__main__':
    # 生成自变量序列x，requires_grad=True代表张量x需要自动微分功能
    x = torch.linspace(-6.5, 3.5, 1000, requires_grad=True)
    y_f = f(x)  # 计算函数f的值
    # 使用backward函数计算f(x)关于x的梯度，梯度值保存在x.grad中
    y_f.sum().backward()  # 因为backward函数只能对标量进行操作，需要先使用y_f.sum将y_f中的元素求和，将其转换为一个标量后，再调用backward计算梯度。

    # 将梯度值x.grad、函数值y_f、自变量x，从pytorch张量转换为numpy数组，转换前需要调用detach函数创建一个原张量的副本（该副本不会跟踪张量的梯度），然后才能正常的将张量转换为numpy数组，而不影响自动梯度的计算。
    y_df = x.grad.detach().numpy()
    y_f = y_f.detach().numpy()
    x = x.detach().numpy()

    # 使用plot绘制图
    plt.plot(x, y_f, label='f(x) = x * x + 3 * x + 2')
    plt.plot(x, y_df, label="f'(x) = 2 * x + 3")
    plt.legend()  # 对图像进行标记
    plt.grid(True)  # 使用grid函数标记出网格线
    plt.show()  # 展示图像

梯度清零

在上面自动微分的代码案例中，只调用了一次 backward 函数，也就是只进行了一次梯度计算。回忆前面学习的梯度下降算法，每次自变量规划下一步路径时都必须重新计算梯度，以便函数值减小的最快方向到达最小值点。也就是说，梯度下降这个过程需要不断的计算梯度，但是在 PyTorch 框架计算中，它默认会累积梯度，因此每次计算梯度都需要调用 grad.zero_() 方法将张量中的梯度清零，这也是梯度下降过程中必须要调用的方法。

方法说明

这里我们使用代码来说明 grad.zero_() 方法的重要性，代码如下：前两次打印结果 $x$ 的梯度值和验证值一样，说明是正确的，但第 3 次打印结果 $x$ 的梯度值和验证值不一样，说明出现了问题。原因就是在调用 backward 前没有清空梯度，而 PyTorch 默认会将梯度累加到已有的梯度上，也就是 $-4+(-4)=-8$。所以如果要使用 backward 重新计算梯度值，需要提前调用grad.zero_() 方法将原来保存的梯度清空，才能确保后续的结果是正确的。

import torch

def f(x): # 定义原函数f
    return x * x - 4 * x - 5

def df(x): # 定义导函数df，导函数用于验证程序的结果
    return 2 * x - 4

# 初始化一个带有梯度的张量
x = torch.tensor([0.0], requires_grad=True)

y = f(x)  # 计算函数值y
y.backward()  # 调用backward计算y关于x的梯度

# 第1次打印（打印结果的梯度值和验证值一样，说明是正确的）
print("x的值:", x.data)              # x的值: tensor([0.])
print("x的梯度值:", x.grad.data)      # x的梯度值: tensor([-4.])
print("验证，x的梯度值:", df(x).data)  # 验证，x的梯度值: tensor([-4.])

# 第2次计算y和梯度前，使用grad.zero将梯度清零
x.grad.zero_()
y = f(x)
y.backward()

# 第2次打印（打印结果的梯度值和验证值一样，说明是正确的）
print("x的值:", x.data)              # x的值: tensor([0.])
print("x的梯度值:", x.grad.data)      # x的梯度值: tensor([-4.])
print("验证，x的梯度值:", df(x).data)  # 验证，x的梯度值: tensor([-4.])

# 第3次计算y和梯度前，不再使用grad.zero将梯度清零
y = f(x)  # 计算函数值
y.backward()  # 计算梯度

# 第3次打印（打印结果的梯度值和验证值不一样，说明出现问题）
print("x的值:", x.data)              # x的值: tensor([0.])
print("x的梯度值:", x.grad.data)      # x的梯度值: tensor([-8.])
print("验证，x的梯度值:", df(x).data)  # 验证，x的梯度值: tensor([-4.])

上手案例

这里我们使用 PyTorch 的自动微分，实现一个求函数 $f(x,y)=x^2+y^2$ 极小值的梯度下降算法，代码如下：

import torch

def f(x, y):  # 定义函数f，计算x^2+y^2
    return x**2 + y**2

x = torch.tensor([1.1], requires_grad=True)  # 初始化自变量x为1.1
y = torch.tensor([2.1], requires_grad=True)  # 初始化自变量y为2.1
n = 100  # 迭代轮数
alpha = 0.05  # 迭代速率，alpha用于控制“一小步”的大小

# 进入梯度下降算法的循环
for i in range(1, n + 1):
    z = f(x, y)  # 计算函数值
    z.backward()  # 调用backward，计算z关于x和y的梯度，计算的梯度值会保存到x.grad和y.grad中
    # 更新x.data和y.data，进行梯度下降算法
    x.data -= alpha * x.grad.data
    y.data -= alpha * y.grad.data
    # 使用zero清除梯度，为下一次迭代做准备
    x.grad.zero_()
    y.grad.zero_()
    # 输出下降信息
    print(f'After {i} iterations, '  # 迭代轮数i
          f'x = {x.item():.3f}, '  # 自变量x
          f'y = {y.item():.3f}, '  # 自变量y
          f'f(x, y) = {z.item():.3f}')  # 函数值f(x,y)

运行上面的代码，可以看到经过 100 轮迭代，找到了在 $x=0$，$y=0$ 处，函数 $f(x,y)$ 取得极小值 $0$ 。