搜索算法

更新: 2025/2/24 字数: 0 字 时长: 0 分钟

搜索算法（searching algorithm）用于在数据结构（例如数组、链表、树或图）中搜索一个或一组满足特定条件的元素。

搜索算法可根据实现思路分为以下两类。

• 通过遍历数据结构来定位目标元素，例如数组、链表、树和图的遍历等。
• 利用数据组织结构或数据包含的先验信息，实现高效元素查找，例如二分查找、哈希查找和二叉搜索树查找等。

暴力搜索

暴力搜索法，也称暴力破解法，是一种非常直观且容易实现但效率低下的方法，即穷尽所有的可能性，找到问题的解，但方法消耗的时间会随着问题规模的扩大而增加，其时间复杂度为 $O(n)$。因此在实际开发过程中，当问题规模比较有限而且可以通过某种方式把候选的解决方案缩小到一定程度的时候，才适合使用该方法求解。

暴力搜索通过遍历数据结构的每个元素来定位目标元素。

• “线性搜索”适用于数组和链表等线性数据结构。它从数据结构的一端开始，逐个访问元素，直到找到目标元素或到达另一端仍没有找到目标元素为止。
• “广度优先搜索”和“深度优先搜索”是图和树的两种遍历策略。广度优先搜索从初始节点开始逐层搜索，由近及远地访问各个节点。深度优先搜索从初始节点开始，沿着一条路径走到头，再回溯并尝试其他路径，直到遍历完整个数据结构。

暴力搜索的优点是简单且通用性好，无须对数据做预处理和借助额外的数据结构。

然而，此类算法的时间复杂度为 $O(n)$ ，其中 $n$ 为元素数量，因此在数据量较大的情况下性能较差。

水仙花数

"""
找出100~999之间的水仙花数
规则：各位数的立方和刚好等于这个数本身
示例：153 = 1^3 + 5^3 + 3^3
"""
for num in range(100, 1000):
    if (num // 100) ** 3 + (num // 10 % 10) ** 3 + (num % 10) ** 3 == num:
        print(num, end=', ')  # 输出：153, 370, 371, 407

寻找完美数

"""
找出1~10000之间的完美数（除自身外所有因子的和等于这个数）
示例：6 = 1 + 2 + 3
"""
# 普通方法
for n in range(1, 10000):
    if n == sum(i for i in range(1, n) if n % i == 0):
        print(n, end=', ')  # 输出：6, 28, 496, 8128

# 快速方法
for n in range(2, 10000):
    total = 1
    for i in range(2, int(n ** 0.5) + 1):
        if n % i == 0:
            total += i
            if i != n // i:
                total += n // i
    if n == total:
        print(total)

百钱百鸡

"""
公鸡5元一只，母鸡3元一只，小鸡1元三只，用100元买100只鸡，有几种买法？
"""
money = 100
for x in range(0, money // 5 + 1):
    for y in range(0, money // 3 + 1):
        z = 100 - x - y
        if z % 3 == 0 and 5 * x + 3 * y + z / 3 == 100:
            print(f'公鸡{x}只，母鸡{y}只，小鸡{z}只。')
'''
输出：
公鸡0只，母鸡25只，小鸡75只。
公鸡4只，母鸡18只，小鸡78只。
公鸡8只，母鸡11只，小鸡81只。
公鸡12只，母鸡4只，小鸡84只。
'''

回溯法

”回溯法“是算法设计中的一种方法，也是暴力搜索法中的一种，它是一种渐进式寻找并构建问题解决方式的策略。通俗讲，当我们在搜索迷宫的时候走到一个死胡同里面了，而且无论如何也找不到正确解的时候，就回到刚才没有走到死胡同的岔路那里，尝试其他的路径，以此类推，最后走出一条正确的道路。以下是维基百科的解释：

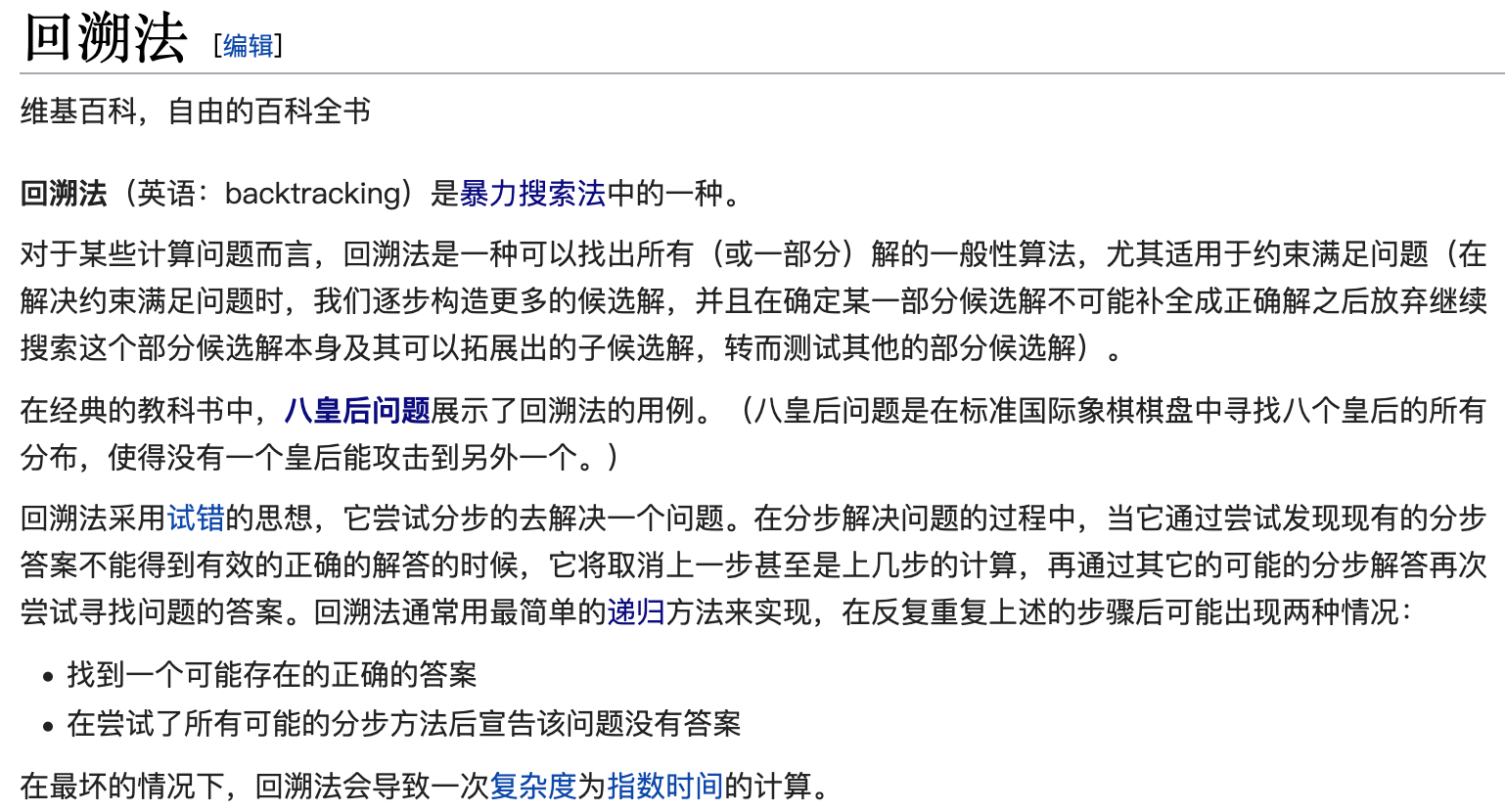
回溯法适合解决有很多分岔路，这些路里面有死路，也有出路的情景问题，而解决方案就是三个重点：

1. 用递归来模拟所有的路；
2. 遇到死胡同的情况就回溯；
3. 出现走通路的情况就返回。

八皇后问题

在国际象棋中有个棋子叫”皇后“，它是攻击力最强的棋子，它可以攻击所在位置的整行、整列、两条斜线所在的棋子。现在的问题是，在棋盘上摆放八个皇后，要求这些皇后相互之间攻击不到对方，问该如何摆放？其中的一组解如下图：

骑士周游

在国际还有一个棋子叫“骑士”，它的走法类似与中国象棋中的”马“，走“日”字形，只不过没有象棋中的“蹩脚马”，问“骑士”怎样不重复的走完一遍 8 X 8 的国际象棋的所有旗格？具体代码如下：

"""
骑士周游
"""
import sys

# 寻找出路（board棋盘，i、i位置横纵坐标，step步数）
def patrol(board, i=0, j=0, step=1):
    # 首先判断下一步的位置是否在棋盘范围内，其次判断下一步是否走过（如果是棋格，则继续走；若是数字，则说明已经走过，函数递归分支结束）
    if 0 <= i < SIZE and 0 <= j < SIZE and board[i][j] == '□':
        board[i][j] = step
        # 通过步数判断是否走完整个棋盘
        if step == SIZE * SIZE:
            # 显示棋盘
            for row in board:
                for col in row:
                    print(f'{col}'.rjust(2, '0'), end=' ')
                print()
            sys.exit(0)
        # 竖“日”字左上到右下
        patrol(board, i + 1, j + 2, step + 1)
        # 横“日”字左上到右下
        patrol(board, i + 2, j + 1, step + 1)
        # 横“日”字左下到右上
        patrol(board, i + 2, j - 1, step + 1)
        # 竖“日”字左下到右上
        patrol(board, i + 1, j - 2, step + 1)
        # 竖“日”字右下到左上
        patrol(board, i - 1, j - 2, step + 1)
        # 横“日”字右下到左上
        patrol(board, i - 2, j - 1, step + 1)
        # 横“日”字右上到左下
        patrol(board, i - 2, j + 1, step + 1)
        # 竖“日”字右上到左下
        patrol(board, i - 1, j + 2, step + 1)
        # 所有下一步节点均走过，当前坐标置为棋格
        board[i][j] = '□'

# 生成8X8大小的棋盘
size = 8
board = [['□'] * size for _ in range(size)]
# 开始周游
patrol(board)
'''
输出：
01 38 59 36 43 48 57 52 
60 35 02 49 58 51 44 47 
39 32 37 42 03 46 53 56 
34 61 40 27 50 55 04 45 
31 10 33 62 41 26 23 54 
18 63 28 11 24 21 14 05 
09 30 19 16 07 12 25 22 
64 17 08 29 20 15 06 13 
'''

逃出迷宫

首先我们来生成一个 10 X 10 大小的迷宫，通过随机数来生成“墙”与“路”，其中在迷宫的左上角代表入口，迷宫的右下角代表出口，为了减少迷宫无出路的情况，因此这两个位置的必定是”路“，具体的代码如下：

"""
迷宫寻路
"""
import random
import sys

# 生成10X10的二维迷宫
size = 10
maze = [['□'] * size for _ in range(size)]
# 遍历每行每列
for row in range(size):
    for col in range(size):
        # 设置入口和出口的路并随机生成墙
        if (row, col) != (0, 0) or (row, col) != (9, 9):
            if random.randint(1, 10) > 7:
                maze[row][col] = '■'
        print(maze[row][col], end='  ')
    print()
'''
输出：
□  ■  ■  ■  ■  ■  ■  ■  ■  □  
□  □  □  □  □  ■  □  ■  □  □  
■  □  ■  □  ■  □  □  □  ■  □  
□  ■  ■  □  □  □  □  ■  ■  □  
□  □  □  □  □  ■  □  □  ■  ■  
■  □  ■  □  ■  □  □  □  ■  □  
■  ■  □  □  ■  □  □  □  ■  ■  
□  □  □  ■  □  □  ■  □  □  □  
□  □  □  □  □  ■  □  □  ■  ■  
■  □  □  □  ■  □  □  □  □  □  
'''

上面的迷宫已经生成好了，可以看到迷宫是有多条出路的，现在我们就要让计算机来寻找其中的一条出路。之前我们讲函数调用的时候讲到，函数会在栈上面保存现场，当调用结束后又会恢复现场，当我们在用回溯法的时候刚好就可以利用“保存现场”、“恢复现场”这个功能，通过函数的调用栈把函数的执行现场保存起来，所以当我们走到死胡同时，我们可以通过函数的调用栈返回之前分叉的节点上去，然后去搜索另外一条路径。具体步骤如下：

1. 首先我们从迷宫的入口进入，坐标为 (0, 0)，步数为 1。
2. 按照”下右上左“试探走法，探索出路。程序首先向下试探，如果下方是“路”，就继续向下试探直到出现”墙“或者到达“边界”才转向，如果下方不是“路”，则向右试探，如果右方是“路”，则到达右方后继续向下试探，如果右方不是“路”，则向上方试探，如果上方不是“路”，则向左方试探，循环往复直到找到出路，否则迷宫无解。

# 寻找出路（maze迷宫，r_index、l_index位置横纵坐标，step步数）
def find_way(maze, r_index=0, l_index=0, step=1):
    # 首先判断下一步的位置是否在迷宫范围内，其次判断下一步是否是路（如果是路，则继续走；若是墙，则行不通，函数递归分支结束；若是数字，则说明已经走过，函数递归分支结束）
    if 0 <= r_index < 10 and 0 <= l_index < 10 and maze[r_index][l_index] == '□':
        # 打上步数标记
        maze[r_index][l_index] = step
        # 判断是否到达出口
        if (r_index, l_index) == (9, 9):
            # 输出迷宫
            for row in range(len(maze)):
                for col in range(len(maze[row])):
                    if isinstance(maze[row][col], int):
                        print(str(maze[row][col]).ljust(2), end='')
                    else:
                        print(maze[row][col], end=' ')
                print()
            # 退出程序
            sys.exit(0)
        # 下方试探
        find_way(maze, r_index + 1, l_index, step + 1)
        # 右方试探
        find_way(maze, r_index, l_index + 1, step + 1)
        # 上方试探
        find_way(maze, r_index - 1, l_index, step + 1)
        # 左方试探
        find_way(maze, r_index, l_index - 1, step + 1)
        # 所有下一步试探都不行，将当前坐标重置为路
        maze[r_index][l_index] = '□'

find_way(maze)
print('没有出路!!!')
'''
输出：
1  ■  ■  ■  ■  ■  ■  ■  ■  □  
2  3  4  5  □  ■  □  ■  □  □  
■  □  ■  6  ■  □  □  □  ■  □  
□  ■  ■  7  □  □  □  ■  ■  □  
□  □  □  8  □  ■  □  □  ■  ■  
■  □  ■  9  ■  □  □  □  ■  □  
■  ■  11 10 ■  20 21 22 ■  ■  
□  □  12 ■  18 19 ■  23 □  □  
□  □  13 16 17 ■  □  24 ■  ■  
■  □  14 15 ■  □  □  25 26 27 
'''